Control de la Calidad Utilizando Excel

Histograma

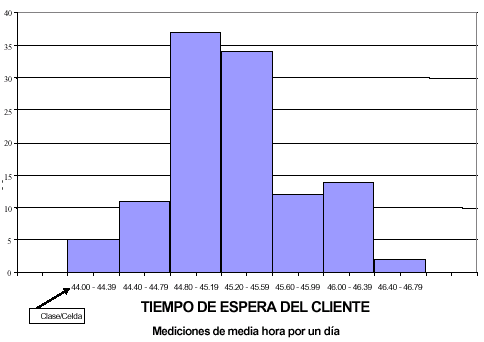
Un Histograma es un tipo especial de gráfica de barras que despliega la variabilidad dentro de un proceso. Un Histograma toma datos variables (tales como alturas, pesos, densidades, tiempo, temperaturas, etc.) y despliega su distribución. Los patrones inusuales o sospechosos pueden inidicar que un proceso necesita investigación para determinar su grado de estabilidad. Ver»

Para diseñar un histograma aplicando la planilla de cálculo Excel, existen dos alternativas:

1. El uso de la Herramienta de análisis histograma
2. El uso de funciones predeterminadas

El uso de la Herramienta de análisis histograma

Microsoft Excel proporciona un conjunto de herramientas para el análisis de los datos.  Algunas de las funciones estadísticas están integradas y otras están disponibles después de instalar las Herramientas para análisis.

Para tener acceso a ellas, haga clic en Análisis de datos en el menú Herramientas.

Si el comando Análisis de datos no está disponible, deberá cargar el programa de complementos de Herramientas para análisis.

Luego de tenerla disponible puede utilizarla sobre algún caso

El uso de funciones para la construcción de un histograma

Función FRECUENCIA

Calcula la frecuencia con que se repiten los valores de un rango y devuelve un matriz vertical de números.

Sintaxis

=FRECUENCIA(datos;grupos)

Datos: es una matriz de un conjunto y valores o una referencia a un conjunto de valores cuyas frecuencias desea contar.

Grupos: es una matriz de intervalos o una referencia a intervalos dentro de los cuales desea agrupar los valores del argumento datos.

Para copiar la función debe situarse en la celda donde se encuentra la función, luego marcar el rango donde se copiará la fórmula, luego (sin dejar de tener el rango marcado) se edita la  función con la tecla "F2", por último se ejecutan las teclas Crt+Shift+Enter.

.

Diagrama de Pareto

Descripción

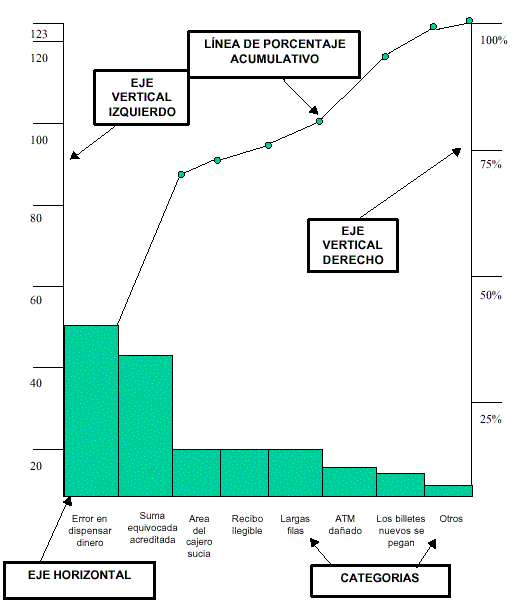
El Diagrama de Pareto consiste en un Histograma cuyas frecuencias se encuentran en orden descendente de izquierda a derecha, conteniendo en el mismo gráfico una curva de frecuencias acumuladas en porcentuales. Ver »

Para su gráfica mediante Excel, se realiza el mismo procedimiento que el análisis de datos por medio del Histograma, y luego se activan las casillas de verificación correspondientes a: Pareto (histograma ordenado) y Porcentaje acumulado de la ventana del Histograma.

Ejercicio

Un fabricante de auto partes, recibió un determinado número de reclamos sobe un determinado producto en el término de una semana. Con el objetivo de mejorar la calidad de su producción y presentación de servicios, se recabaron los datos referentes a estos reclamos, organizándolos en categorías.

Agrupando en clases

Cuando los datos provenientes del estudio de un problema son agrupados, la visualización de la distribución de los mismo se vuelve mas clara.

Para ello los datos deben agruparse por clase y determinar cuál es la frecuencia de ocurrencia para cada intervalo de clase.

Una forma de determinar la amplitud de clase para un estudio en particular es la resultante de dividir la diferencia entre el valor máximo y el valor mínimo por la raíz cuadrada de la cantidad de elementos que conforman el estudio.

Contando con dichos valores ya pueden ser utilizados para la construcción de un Histograma.

Diagrama de Dispersión

Fuerza de la relación lineal entre dos variables

El diagrama de correlación es una representación gráfica en un eje de coordenadas de los datos que se recogen sobre dos variables para poder estudiar si existe relación de causa efecto entre ellas (Kume 1985b). Se utiliza para comprender si se encuentran vinculadas entre sí dos magnitudes y en qué medida. Sirve para verificar causas reales, definir y medir relaciones existentes entre dos variables.

Análisis de correlación: se usa un gupo de técnicas estadísticas para medir la fuerza de la relación (correlación) entre dos variables.
Diagrama de dispersión: gráfica que describe la relación entre las dos variables de interés.
Variable dependiente: la variable que se pronostica o estima.
Variable independiente: la variable que proporciona la base para la estimación. Es la variable predictora.

El coeficiente de correlación (r) es una medida de la intensidad de la relación entre dos variables. Requiere datos con escala de intervalo o de razón (variables). Puede tomar valores entre -1.00 y 1.00. Valores de -1.00 o 1.00 indican correlación fuerte y perfecta. Valores cercanos a 0.0 indican correlación débil. Valores negativos indican una relación inversa y valores positivos indican una relación directa.

Ver »

.

En el Vínculo Herramientas del asistente del Excel dentro de la herramienta Análisis de datos encontrará el aplicativo Regresión que le permitirá graficar los valores de las variables componentes del estudio. 

Gráficos de control

Descripción

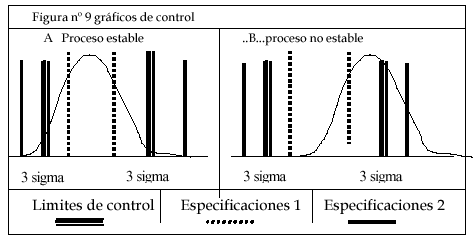
Los gráficos de control son una herramienta para medir si el proceso se encuentra dentro de los límites deseados. Su aplicación más frecuente es en los procesos industriales, aunque  son válidos para cualquier proceso en toda organización. Son un diagrama, donde se van anotando los valores sucesivos de la característica de calidad que se está controlando los datos se registran durante el funcionamiento y a medida que se obtienen.

El gráfico de control típico muestra tres líneas paralelas al eje de las "X", a saber:

• Línea Central, que representa el valor medio de calidad exigido por la fábrica.
• Línea Superior, que representa el Límite Superior de Control (LSC).
• Línea Inferior, que representa el Límite Inferior de Control (LIC).

Por lo tanto, el desempeño del proceso a través del tiempo estará dentro de los parámetros aceptables cuando todos los puntos del gráfico están entre el el Límite Superior de Control (LSC) y el Límite Inferior de Control (LIC) y dicha disposición sea aleatoria.

Existen dos tipos de gráficos de control, para:

• Atributos, aplicable a estudios de comportamiento de números y proporciones.
• Variables, aplicables a problemas de peso, densidad, concentración, etc.

Ver »

Gráfico de control para atributos

Es uno de los gráficos para atributos mas utilizado, el cual permite monitorear la variación del número de ítems defectuosos en una muestra de tamaño constante.

Ejemplo:

Donde,

n: tamaño de la muestra (constante);
d: número de piezas defectuosas en cada muestra;
p: proporción de piezas defectuosas por muestra ( p = d / n ).

Para la construcción del gráfico es preciso conocer:

• la media de las proporcione,
• el número medio,
• los valores de LSC,
• los valores de LIC.

La media de las proporcione

P = media de las proporciones

m = número de muestras

Sumatoria de las proporciones

m = 6

P = 1/6 * (B4 + C4 + D4 + E4 + F4 + G4)  => P = 0,041666667
 

Número medio:

NP = P x n
NP = número medio;
n   = tamaño de la muestra ( n = 100 )
NP = 0,04167 * 100 
NP = 4,166666667

Limite Superior de Control

LSC = Limite Superior de Control
NP   = Número medio
P     = Medias de las proporciones
 

LSC= B18+(3*(B18*(1-B12))^(1/2)) => LSC= 10,16145607
 

Limite Inferior de Control

LIC= =B18-(3*(B18*(1-B12))^(1/2)) => LIC= -1,828122737
 

Como el límite inferior de control no puede ser un número negativo, se asume como LIC el menor valor posible, por tanto

LIC = 0.
 

construcción del gráfico

Gráfico de control para variables

El gráfico de variable más conocido es el gráfico X-R, que monitorea la variación de la media y amplitud de los datos a lo largo del tiempo. 

Ejemplo VIEIRA (1995):

Una cooperativa agrícola que produce, embolsa y comercializa café torrado y molido, resolvió verificar la calidad de su producto en relación al peso de cada paquete.

Para ello, necesario un gráfico de control para variables, que en este caso, es el peso de los paquete. En el estudio fue realizada una muestra aleatoria de cuatro paquetes en cada una de las seis muestras.

Para cada una de las seis muestras se calculó la media aritmética y la amplitud de los pesos (valor máximo - valor mínimo).

En la construcción del gráfico X - r son necesarios los siguientes valores:

• Media de las medias de las muestras (X);
• Media de las amplitudes de las muestras (K);
• Tamaño de las muestras (n);
• Límite Superior de control (LSC);
• Límite Inferior de control (LIC).

Estudio

Número de muestras (m) = 6

Número de paquetes por muestra (n) = 4

Colecta de Datos:

Cálculo da média:
 

X = sumatoria de la muestra 1 / n

donde,

X = media aritmética;

Sn = son dos pesos de la muestra 1

n = tamaño de la muestra

X = 250 / 4

X = 62,5  (=SUMA((B3:B6))/CONTAR(B3:B6))

Cálculo de la amplitud de los pesos:

r = valor máximo - valor mínimo

donde,

r = amplitud

r = 70 - 55

r = 15    <  =MAX(B3:B6)-MIN(B3:B6)  >

Construcción de la tabla:

Ahora, para calcular los limites de control LIC y LSC se debe obtener las medias de las medias aritméticas y de las amplitudes de todas las muestras.

Media de las medias (X) = Sumatoria med / m

X = 367,50 / 6

X = 61,25   <  =SUMA(B7:G7)/CONTAR(B7:G7)  >

Media de las amplitudes (K) = Sumatoria ampl. / m

K = 95 / 6

K = 15,83   < =SUMA(B8:G8)/CONTAR(B8:G8)  >
 

LIC = X - A2 x K

LSC = X + A2 x K
 

LIC = 61,25 - (0,729 x 15,83)

LIC = 49,71

LSC = 61,25 + (0,729 x 15,83)

LSC = 72,79

.