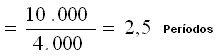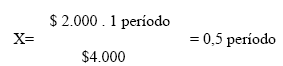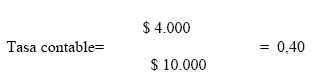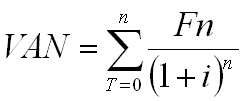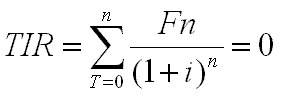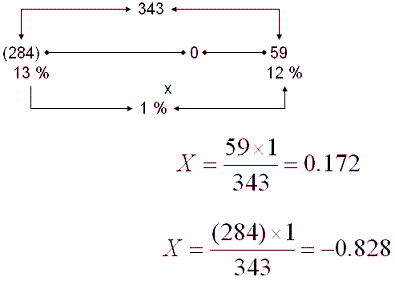Evaluación de inversiones: de la teoría a la práctica

1.- Presentación

Este capítulo incluye el tratamiento del análisis de inversiones, como prólogo a la definición práctica de escenarios futuros. En una segunda entrega se presentará el análisis de riesgo aplicando modelos de simulación y la problemática al análisis de inversión con tasas de descuento inciertas.

Citando algunas confusiones entre los niveles teóricos y prácticos, el autor espera achicar la brecha entre las acciones de los ejecutivos en ejercicio y las exposiciones brillantes pero inexpertas.

2.- Introducción

Es habitual en las personas que inician sus estudios de administración, que éstos relacionen la idea de planificación con una abstracción teórica; pocas cosas más alejadas de la realidad. La planificación se desarrolla como un continuo ejercicio de opciones, en las que en forma explícita o implícita definimos escenarios, en los cuales, en mayor o menor grado, influiremos a partir del grado de proactividad con que diseñemos nuestras estrategias.

3.- Evaluación de proyectos de inversión

La evaluación de inversiones de capital es el estudio y aceptación de proyectos de aplicación de recursos, cuyos beneficios se esperan recibir en un momento futuro (James Van Horne, 1976).

La evaluación de inversiones implica formular proyectos de inversión, estimar sus posibles flujos de fondos y evaluarlos, seleccionar proyectos según un adecuado criterio de aceptación y finalmente reevaluarlos sistemáticamente después de haberlos aceptado (James Van Horne, 1976).

Las inversiones pueden provenir de nuevos proyectos, de reemplazos de equipos, de resultas de actividades de investigación y desarrollo, etc., pero abstracción hecha de las particularidades de cada uno de los rubros posibles, existen criterios que se fundan en el análisis técnico del flujo estimado de fondos que proporcionan información importante para encarar la decisión de aceptar o rechazar una determinada opción.

3.1.- El flujo de fondos

La tarea de evaluación se efectúa a partir de la determinación del flujo neto de fondos, suma algebraica de egresos e ingresos netos, sin considerar aquellos costos que resulten no erogativos, o sea que no originen desembolso real de dinero, debiendo considerar en cambio la incidencia impositiva que dichos costos ocasionan, ya que esta incidencia repercute concretamente en la determinación de flujos de fondos. En otras palabras, nos estamos refiriendo a una proyección futura de un flujo de caja.

Se hace mención al flujo neto de efectivo porque sólo los fondos líquidos pueden ser invertidos con el objetivo de obtener en el futuro una suma superior. Destacamos el término de futuro, porque en este tipo de análisis se parte, en el mejor de los casos, de una inversión realizada en el momento actual para compararla con los ingresos futuros que esperamos obtener de ella.

A título de ejemplo, se presenta un flujo neto de fondos, con el objetivo de clarificar la notación utilizada. Si, por ejemplo se quisiera analizar la conveniencia de realizar una inversión que demanda un egreso inicial de $ 10.000, con ingresos futuros estimados del orden de los $ 4.000 a percibir a los 30, 60 y 90 días de efectuada la inversión inicial, podría ser plantearlo de este modo:

o bien

La estructura de la presentación horizontal o vertical del cuadro es indistinta. Los flujos negativos se denotan encerrándolos entre paréntesis, y en este caso el egreso inicial se encuentra ubicado en el período 0 para definir el momento actual, y los momentos 1, 2 y 3, que definen los tres plazos en que se esperan recibir los ingresos. En general, esto sucede en las operaciones financieras, en las que se pacta una determinada fecha para el recupero del dinero. Pero la operación de una empresa en marcha, no obedece al mismo criterio, debiendo entonces homogeneizarse en la presentación el conjunto de fondos generados dentro de un lapso determinado. Si ésta fuera la situación, el ejemplo anterior quedaría:

4.- Métodos para la evaluación

4.1.- Período de Repago o Recupero Simple

Consiste en establecer en cuánto tiempo se recupera una inversión dada. Si los ingresos futuros fueran iguales para todos los períodos, el cálculo se realizaría estableciendo el cociente entre la inversión inicial y el promedio de ingresos netos. En el ejemplo anterior sería:

Período de Repago

Para el caso en que los ingresos futuros fueran irregulares, el cálculo se realiza sumando algebraicamente el importe del primer período al egreso inicial, y si el resultado continúa siendo negativo, sumando el valor del segundo período, hasta encontrar un resultado negativo que sea menor en términos absolutos que el valor positivo del próximo período. Una vez obtenido, y ante la ausencia de datos ciertos, podemos asumir que los ingresos futuros se repartirán en forma homogénea a través del tiempo, y elaborar una simple regla de tres para calcular la fracción de período que restaría para completar el recupero. Tomemos, por ejemplo la siguiente situación:

Podemos advertir que siguiendo el criterio expresado, al cabo del período 1-2, hemos recuperado $ 8.000 de los $ 10.000 invertidos inicialmente, motivo por el cual sabemos que los $ 2.000 restantes se recuperarán dentro del período 2-3. Si asumiéramos que los ingresos de $4.000 del período 2-3 se distribuyen en forma regular a lo largo del mismo, podríamos decir:

Luego, el recupero de la inversión inicial se produjo en 2,5 períodos.

Restricciones del método Período de Repago

El método Período de Repago, no toma en cuenta el valor tiempo del dinero; llamamos así a la capacidad que tiene un capital de generar una rentabilidad, abstracción hecha, por ahora, del concepto de inflación.

Así:

Como podemos apreciar, la alternativa A es superior a la B, por cuanto recupera en el período 0-1 $ 2.000 más que la B, permitiendo entonces obtener un mayor rendimiento por la colocación de esa suma. No obstante, el método del período de recupero da iguales resultados para ambas alternativas, verificándose, de ese modo, la primera de las restricciones, que, como veremos más adelante, puede salvarse por medio de un artificio técnico que permite incorporar al análisis la noción de valor tiempo, convirtiendo al método en una herramienta útil para la toma de decisiones.

Otra restricción radica en que no considera lo que sucede una vez recuperada la inversión inicial. Ejemplificamos:

En el ejemplo anterior, en ambas alternativas se recupera el capital inicial invertido al finalizar el período 1-2, pero en la alternativa A en el período 2-3 obtiene un ingreso superior a la alternativa B.

Queda claro que las restricciones señaladas, al ser consideradas, no comprometen la validez de este recurso con que contamos para evaluar inversiones.

4.2.- Tasa Contable de Ganancia

También llamada Rentabilidad según Libros, resulta de dividir la utilidad media correspondiente al período por la inversión inicial. En principio es un método de origen contable, pues trabaja a partir de la utilidad, calculada de forma convencional, diferenciándose de los otros que trabajan a partir del flujo financiero.

Observaciones al método Tasa Contable de Ganancia

Adicionalmente al hecho de ponderar a la inversión inicial con la utilidad media, se suma que las utilidades obtenidas en los distintos períodos sufren el mismo tratamiento, desconsiderando así el valor del dinero en el tiempo.

En el ejemplo podemos apreciar que la alternativa A es significativamente superior a la B, a partir de la distinta distribución de las utilidades futuras estimadas, pero el resultado que arroja el método es el mismo para ambas alternativas, ya que el promedio de utilidades futuras, $ 4.000, es igual para ambas a pesar de la diferente distribución que ambas alternativas ofrecen. La facilidad de cálculo de este método no debería ser una preorización del mismo, menos aún dejar de considerar sus restricciones.

4.3.- Valor Actual Neto

El Valor Actual Neto (V.A.N.) consiste en llevar el flujo futuro de fondos a términos de moneda del momento inicial. Esto se consigue por medio de la aplicación a cada uno de los valores del flujo de fondos del coeficiente surgido de la fórmula de actualización, y sumando luego algebraicamente los resultados:

Donde Fn representa a cada valor del flujo futuro de fondos, "i" corresponde a la tasa de interés de descuento y "n" representa los períodos correspondientes al flujo de fondos. Ejemplifiquemos, suponiendo una tasa de descuento del 10 % .

Valor Actual Neto = 177

En principio cabría aceptar este proyecto, ya que el Valor Actual Neto es positivo, o sea que descontado el flujo de fondos con el objetivo de llevarlo a moneda homogénea del momento 0, el flujo descontado sumado algebraicamente da positivo.

El significado que ese valor de $ 177 tiene, implica que una vez cubiertos el egreso inicial y los costos financieros del proyecto, quedan como remanente $ 177 en términos de moneda del momento inicial. La aceptación debe referirse a la consideración que hagamos de un conjunto de circunstancias que rodean al proyecto, pero en principio el mismo parecería aceptable.

Ciertas consideraciones a tener en cuenta, en algunas ocasiones, al momento de definir la tasa de corte.

Respecto de lo que se expresaba al desarrollar el período de recupero, existe la posibilidad de analizar el retorno de una inversión dada a partir del flujo de fondos actualizado que se obtuvo para alcanzar el Valor Actual Neto. De esta forma, se evita una de las restricciones del método, que es el no considerar el valor tiempo del dinero, y se transforma en una importante herramienta para la toma de las decisiones.

Para épocas en donde el riesgo de cambios que rompan con lo establecido es muy grande, el período de repago a valores descontados es un esquema de análisis que no se puede obviar.

4.4.- Tasa Interna de Retorno

Ezra Solomon (1969) define a la Tasa Interna de Retorno (T.I.R.) como la verdadera tasa a la cual una inversión es recuperada por los ingresos generados por un proyecto. Operativamente, consiste en llevar a 0 la suma del flujo futuro de fondos.

Es aquella tasa a la cual los ingresos incrementales que se esperan de un proyecto tienen un valor descontado exactamente igual al valor descontado de todos los egresos de fondos incrementales en que hay que incurrir para encarar un determinado proyecto.

A continuación se presenta un ejemplo práctico, que por ser el mismo con que se trabajó el V.A.N., se sabe que presenta un valor actual neto de $ 177 a una tasa de descuento del 10 %, por lo cual igualar a 0 el flujo neto de fondos impondrá trabajar con una tasa mayor. Se prueba entonces con el 12 %, tasa a la cual se acerca al resultado, ya que presenta un valor final de $ 59. Se Debe volver a incrementar la tasa, y entonces se utiliza el 13 %

La Tasa Interna de Retorno debe igualar a 0 el flujo de fondos. En el caso que se acaban de ver, puede apreciarse que la T.I.R. se sitúa entre el 12 y el 13 %, pudiendo aproximarnos a la respuesta a través de un simple ejercicio de interpolación.

La tasa interna de retorno del proyecto surgirá de sumarle a 12 % el 0,172 %, o de restarle a 13 % el 0,828 %. Luego, el resultado es 12,172 %, que es el rendimiento del proyecto, y contra el cual debemos comparar el costo de financiación del mismo.

Teniendo en cuenta los aspectos teóricos tratados, y los ejemplos prácticos en ellos basados, podemos decir que la diferencia técnica en los fundamentos del Valor Actual Neto y la Tasa Interna de Retorno se reduce simplemente a una forma de expresión diferente de los resultados. En tanto a través de la tasa interna de retorno se arriba a un resultado expresado en términos porcentuales, el Valor Actual Neto lo hace con un valor porcentual, la tasa de descuento y un valor absoluto, justamente el Valor Actual Neto.

5.- Diferencia entre Valor Actual Neto y Tasa Interna de Retorno

Es bastante corriente que algunos autores, como Solomon o el mismo Van Horne teoricen sobre la ventaja técnica relativa que el valor actual neto tendría sobre la tasa interna de retorno.

James Van Horne (1976) en Administración Financiera, presenta el siguiente ejemplo a partir del cual ensaya una teoría acerca de la superioridad del VAN sobre la TIR:

k = 10 % (tasa de corte)

Se trata de dos proyectos mutuamente excluyentes con períodos de vida útil de la misma duración. Pero tienen una particularidad: en tanto el proyecto A es preferible si nos guiamos por TIR, el proyecto B es el que debemos elegir si nos guiamos por el VAN.

James Van Horne (1976) sostiene que dadas las diferentes tasas de reinversión implícitas (10 % para el VAN, y 25 % para el A y 22 % para el B en el caso de la TIR), es más prudente elegir el método que supone la reinversión de los flujos futuros a tasa más baja. Escribe: "Con el método TIR, la tasa implícita de reinversión es diferente para cada proyecto. Con el método VAN, en cambio, la tasa implícita de reinversión, (que es la tasa de corte) es la misma para todos los proyectos".

A nuestro entender, la variable más eficiente para fijar la tasa de corte es el costo financiero marginal, y éste no es necesariamente coincidente en todas las ocasiones.

Analizando el ejemplo presentado: la primer observación que surge es la enorme diferencia entre la tasa de costo financiero, (10 %), y los rendimientos estimados para ambos proyectos (25 y 22 %). Dichos rendimientos no pueden estar exentos de una importante dosis de riesgo, que es fácilmente comprensible en un contexto de inestabilidad, pero que también debe ser considerado a partir de que en la actualidad la estabilidad de las variables económicas no es sinónimo de crecimiento permanente y lineal de los distintos mercados.

Por el contrario, a partir de la crisis del petróleo de 1.973, los mercados detuvieron su crecimiento, para luego convertirse en decrecientes a partir de 1.977-78. En ese contexto, el riesgo no es condición exclusiva de quienes operan en países signados por la inestabilidad y las recurrentes crisis económicas, pasando a ser una característica propia de cualquier mercado. ¿Quién puede asegurar la no aparición de un nuevo producto que rápidamente transforme en obsoleto el propio? Ante esta circunstancia el período de repago a valores actualizados pasa a constituirse en una herramienta importante a la hora de decidir inversiones.

Por este motivo, se cree que el proyecto A es superior al B, pero no por ser mejor su tasa interna de retorno, sino porque lo es su período de repago a valores descontados.

Concluyendo se puede decir que para que la tasa interna de retorno y el valor actual neto nos conduzcan a decisiones diferentes respecto de la elección entre dos proyectos alternativos, como es el caso del ejemplo, deben verificarse dos condiciones:

1) Distribución marcadamente distinta entre los ingresos futuros de ambos flujos de fondos.

2) Tasas de costo financiero y de rendimiento del proyecto con enormes diferencias entre sí, lo que implica necesariamente una alta dosis de riesgo.

Cuando esto sucede, se debería decidir a partir del análisis del período de repago a valores descontados.

En cuanto al concepto de que el VAN es una medida más prudente (James Van Horne, 1976), se debería tener cierta prudencia. En realidad, decidir a partir de la consideración de los resultados que el mismo arroja en casos como el anterior conlleva un gran riesgo, ya que la importante tasa de rendimiento ofrecida nos lleva a privilegiar ingenuamente aquel proyecto que menos efectivo retorne en el mediano y corto plazo, en la medida que recuperarlo implicaría tener que recolocarlo en otro proyecto, no siendo factible encontrar otra tasa de semejante nivel.

Como la TIR presupone para ser real la recolocación de los fondos recuperados a la tasa de rendimiento del proyecto, y el VAN lo hace a la tasa de corte, esto es la tasa de costo financiero, convendría, forzando la interpretación de Van Horne (1976) y Solomon (1969), no recuperar rápidamente los fondos para no afrontar el problema de recolocarlos. 

Aquellas administradores que hayan tenido alguna responsabilidad de manejo financiero saben que esto es una utopía que se sostiene sólo a partir de no considerar la incidencia del riesgo, que aumenta en la medida que más largo es el plazo de recupero.

La tasa interna de retorno y el valor actual neto, en condiciones normales, proporcionan la misma orientación en la toma de decisiones financieras, no ofreciendo desde nuestro punto de vista ventajas técnica significativas el uno sobre el otro.

Es poco fructífero discutir acerca de la ventaja relativa de un método sobre otro con el objetivo de recomendar la utilización del primero sobre el segundo. Las decisiones de inversión son habitualmente lo suficientemente complejas para obligarnos a echar mano a toda la información de que disponemos para encarar la apuesta que significan, con la mayor cantidad de información posible, y cada uno de los métodos nos dice algo distinto de los otros. Lo importante es la capacidad que hemos desarrollado para interpretarla.

El español Bernardino Herrero Nieto ha escrito: "El hombre débil y el dirigente mediocre, sucumbe no por ser débil o mediocre, sino por ignorar que lo es". Salvando las distancias, con los métodos para evaluar inversiones sucede lo mismo: si se conocen en profundidad todas las limitaciones que tienen, podremos aprovechar realmente toda la información que nos proporcionan y nos serán de invalorable utilidad en la apasionante tarea de decidir la aceptación o rechazo de inversiones.

6.-  Conclusión

Los métodos para evaluar inversiones comenzaron a popularizarse en Argentina a través de su utilización por parte de compañías extranjeras en las décadas de los cincuenta y sesenta del siglo pasado. A este hecho es dable atribuir el que durante años se trabajara el análisis de flujos de fondo en moneda extranjera: las casas matrices solicitaban esa información traducida a moneda dura.

Pero durante años se atribuyó algún grado de seguridad adicional al hecho de preparar los flujos de fondos predominantemente en dólares. Queda claro que dicha circunstancia no mejora ni empeora el análisis, ya que lo que se pretendía evitar era la distorsión que acaecía en función de las fluctuaciones que sufría nuestra economía.

Demás está decir que dichos cambios incidían significativamente sobre las evaluaciones y las decisiones que en función de ellas se tomaban, pero que la expresión en moneda extranjera del flujo de fondos no resultaba de ninguna manera una solución para la situación. Expresar todo en dólares de un determinado valor equivale a dividir el flujo de fondos por una constante, con lo cual los resultados van a ser exactamente los mismos. Lo interesante en este caso sería poder predecir el valor relativo de la moneda extranjera respecto de la nuestra a través del lapso que dure la vida útil del proyecto, para establecer su incidencia sobre los distintos conceptos que constituyen los costos del mismo, lo que supone un ejercicio de futurología sin seriedad técnica.

En lo que hace al problema inflacionario, el mismo incide no por los incrementos absolutos de las variables que consideramos en los proyectos, sino por las distorsiones en los niveles relativos de los distintos costos a considerar.

En la medida que aludimos a los problemas que la inestabilidad de las variables económicas provocan, debemos tener en cuenta que dichas distorsiones afectan más, en general, el análisis de proyectos industriales que los de índole financiera, ya que normalmente aquellos requieren para su recupero un lapso mucho mayor, exponiéndose así durante más tiempo a las modificaciones que sufra la economía que los contiene.