Research article

Evaluación de estructuras métricas con Unidades de Procesamiento Gráfico de Propósito General

Evaluating metric structures with General Purpose Graphic Processing Units

Resumen

La búsqueda por similitud consiste en recuperar todos aquellos objetos dentro de una base de datos que sean parecidos o relevantes a una determinada consulta. Actualmente es un tema de gran interés para la comunidad científica debido a sus múltiples campos de aplicación, como la búsqueda de palabras e imágenes en la World Wide Web, reconocimiento de patrones, detección de plagio, bases de datos multimedia, entre otros. La búsqueda por similitud o en proximidad se modela matemáticamente a través de un espacio métrico, en el cual los objetos son representados como una caja negra donde la única información disponible es la distancia de este objeto a los otros. En general, el cálculo de la función de distancia es costoso y los sistemas de búsqueda operan a una gran tasa de consultas por unidad de tiempo. A fin de optimizar este procesamiento se han desarrollado numerosas estructuras métricas, que funcionan como índices y realizan un preprocesamiento de los datos a fin de disminuir las evaluaciones de distancia al momento de la búsqueda. Por otro lado, la necesidad de procesar grandes volúmenes de datos hace poco factible la utilización de una estructura en aplicaciones reales si ésta no considera la utilización de entornos de procesamiento paralelo. Existen una serie de tecnologías para realizar implementaciones de procesamiento paralelo. Se incluyen entre las más vigentes las tecnologías basadas en arquitecturas multi-CPU (multi-core) y GPU / multi-GPU, que son interesantes debido a las altas prestaciones y los bajos costes involucrados. En el presente artículo se aborda la búsqueda por similitud y la implementación de estructuras métricas sobre entornos paralelos. En la sección 2 se presenta el estado del arte en los temas relacionados a búsqueda por similitud con estructuras métricas y tecnologías de paralelización. Se proponen análisis comparativos sobre experimentos que buscan identificar el comportamiento de un conjunto de espacios métricos y estructuras métricas seleccionados sobre plataformas de procesamiento basadas en multicore y GPU en la sección 3. Finalmente, se recopilan las conclusiones obtenidas y sugerencias de trabajos futuros en la sección 4.

Abstract

Similarity search consists on retrieving objects within a database that are similar or relevant to a particular query. It is a topic of great interest to scientific community because of its many fields of application, such as searching for words and images on the World Wide Web, pattern recognition, detection of plagiarism, multimedia databases, among others. Search by similarity or proximity mathematically modeled through a metric space in which objects are represented as a black box where the only information available is the distance from the object to the other. In general, the calculation of the distance function is costly and search systems operate at a high query rate per unit time. To optimize this process have been developed numerous metric structures that function as indexes and perform preprocessing of data to decrease the distance evaluations when the search. Furthermore, the need to process large volumes of data makes unfeasible the use of a structure in real applications if it does not consider the use of parallel processing environments. There are a number of technologies for parallel processing implementations. Technologies based on multi-CPU (multi-core) and GPU / multi-GPU architectures that are interesting due to the high performance and low costs involved. In this article the similarity search and implementation of metric structures on parallel environments is addressed. In section 2 the state of the art is presented on issues related to search by similarity metric structures and parallelization technologies. Comparative analysis of experiments seeking to identify the behavior of a set of metric spaces and metric structures on selected processing platforms based on multicore and GPU in the proposed section 3. Finally, the conclusions and suggestions for future work are summarized in section 4.

Palabras Clave:

Búsquedas por similitud, espacios métricos, estructuras métricas ⓘ

Keyword:

Similarity search, metric spaces, metric structures parallel processing ⓘ

Introducción

La búsqueda de objetos similares sobre un gran conjunto de datos se ha convertido en una línea de investigación de gran interés. Aplicaciones de estas técnicas pueden ser encontradas en reconocimiento de voz e imagen, en problemas de minería de datos, detección de plagios y muchas otras.

En general, se utilizan diversas estructuras de datos con vistas a mejorar la eficiencia en términos de los cálculos de distancia, comparados con la búsqueda secuencial dentro de la base de datos (conocido como algoritmo fuerza bruta). Por otro lado, se busca reducir los costos en términos de tiempo mediante el procesamiento en paralelo de grandes volúmenes de datos [GKKG03].

xisten una serie de tecnologías para realizar implementaciones de procesamiento paralelo. Se incluyen entre las más vigentes las tecnologías basadas en arquitecturas multi-CPU, GPU y multi-GPU. En este sentido, la aplicación de estas nuevas tecnologías sobre búsquedas por similitud en espacios métricos [HPCS11] [JISBD12] permiten un alto nivel de paralelismo a un muy bajo coste.

Búsquedas por Similitud en Espacios Métricos

La búsqueda por similitud consiste en la búsqueda de objetos más similares a través de una búsqueda por rango o de vecinos más cercanos en un espacio métrico. Se puede definir un espacio métrico como un conjunto Χ con una función de distancia d:X2→ R, tal que ∀ x,y,z ∈, se deben cumplir las propiedades de: positividad (d(x,y)>=0 y d(x,y)=0 ssi x=y), simetría (d(x,y)=d(y,x)) y desigualdad triangular (d(x,y)+d(y,z)>=d(x,z)).

Sobre un espacio métrico (X,d) y un conjunto de datos finito Y ⊂ X, se puede realizar una serie de consultas. La consulta básica es la consulta por rango. Sea un objeto x ∈ X, y un rango r ∈ R. La consulta de rango alrededor de x con rango r es el conjunto de puntos y ∈ Y, tal que d(x,y)<= r. Un segundo tipo de consulta, que puede construirse usando la consulta por rango, es los k vecinos más cercanos. Sea un objeto x ∈ X,  y un entero k. Los k vecinos más cercanos a x son un subconjunto A de objetos de Y, donde |A|=k y no existe un objeto y∈ A tal que d(y,x) sea menor a la distancia de algún objeto de A a x.

El objetivo de los algoritmos de búsqueda es minimizar la cantidad de evaluaciones de distancia realizadas para resolver la consulta. Los métodos para buscar en espacios métricos se basan principalmente en dividir el espacio empleando la distancia a uno o más objetos seleccionados. El no trabajar con las características particulares de cada aplicación tiene la ventaja de ser más general, pues los algoritmos funcionan con cualquier tipo de objeto [ACM01].

Estructuras Métricas de Búsqueda

Existen distintas estructuras para buscar en espacios métricos, las cuales pueden utilizar funciones discretas o continuas de distancia. Su objetivo es reducir las evaluaciones de distancias durante la búsqueda, y con ello disminuir el tiempo de procesamiento. Algunas de las estructuras basan la búsqueda en clustering y otras en pivotes.

Los algoritmos basados en clustering dividen el espacio en áreas, donde cada área tiene un centro. Se almacena alguna información sobre el área que permita descartar toda el área mediante sólo comparar la consulta con su centro. Los algoritmos de clustering son los mejores para espacios de alta dimensión, que es el problema más difícil en la práctica. Algunos ejemplos de estructuras son GNAT [VLDB95], M-Tree [VLDB97], SAT [VLDBJ02], Slim-Tree [TTSF00], EGNAT [SISAP09] y otros [ACM01].

En el segundo caso, se seleccionan pivotes del conjunto de datos y se precalculan las distancias entre los elementos y los pivotes. Cuando se realiza una consulta, se calcula la distancia de la consulta a los pivotes y se usa la desigualdad triangular para descartar candidatos. En los métodos basados en pivotes, se selecciona un conjunto de pivotes y se precalculan las distancias entre los pivotes y todos los elementos de la base de datos. Los pivotes sirven para filtrar objetos en una consulta utilizando la desigualdad triangular, sin medir realmente la distancia entre el objeto consulta y los objetos descartados.

1. Sea {p1, p2, ..., pk} X un conjunto de pivotes. Para cada elemento y de la base de datos Y , se almacena su distancia a los k pivotes (d(x, p1), ..., d(x, pk)). Dada una consulta q y un rango r, se calcula su distancia a los k pivotes (d(q, p1), ..., d(q, pk)).
2. Si para algún pivote pi se cumple que | d(q, pi) – d(x, pi) | > r, entonces por desigualdad triangular se tiene que d(q, x) > r; por lo tanto, no es necesario evaluar explícitamente d(x, q). Todos los objetos que no se puedan descartar por esta regla deben ser comparados directamente con la consulta q.

Algunas estructuras de este tipo son: LAESA [MOV94], FQT y sus variantes [CPM94], Spaghettis y sus variantes [SPIRE99] [NN97], FQA [CMN01], SSS-Index [SOFSEM07] y otros [ICCSDE12].

Una estructura métrica genérica (Generic Metric Structure: GMS) puede considerarse como una tabla de distancias entre los pivotes y todos los elementos de la base de datos. Es decir, cada celda almacena la distancia d(yi, pj) siendo yi un elemento de la base de datos. El algoritmo para la búsqueda por rango sobre esta estructura, dada una consulta q y un rango r, sería:

1. Para cada consulta q, se calcula la distancia entre q y todos los pivotes p1, ... , pk. Con esto se obtienen k intervalos de la forma [a1, b1], ..., [ak, bk], donde ai = d(pi, q) − r y bi = d(pi, q) + r.
2. Los objetos, representados en la estructura por sus distancias a los pivotes, son candidatos a la consulta q si todas sus distancias están dentro de todos los intervalos.
3. Para cada candidato y, se calcula la distancia d(q, y), y si d(q, y) <= r, entonces el objeto y es solución a la consulta q.

La Figura 1 representa una estructura GMS construida con 4 pivotes. Para cada consulta q con distancias a los pivotes d(q,pi) = {8, 7, 4, 6} y un rango de búsqueda r = 2, se definen los intervalos {(6, 10), (5, 9), (2, 6), (4, 8)}. Las celdas marcadas en gris oscuro son aquellas que están dentro del intervalo de búsqueda. Las celdas tachadas con líneas son los objetos candidatos (2, 13 y 15), que serán evaluados directamente con la consulta.

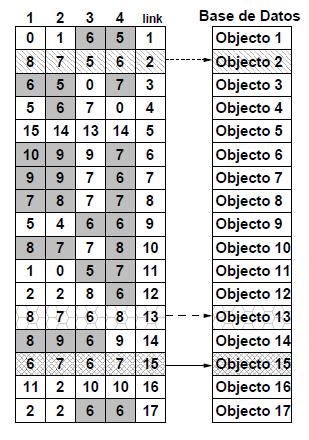Figura 1. Búsqueda sobre una estructura métrica genérica (GMS)

Plataformas Paralelas de Memoria Compartida

Actualmente, existe una gran variedad de plataformas paralelas sobre las cuales se pueden implementar estructuras métricas. En este contexto, muchos estudios se han enfocado inicialmente en plataformas de memoria distribuida usando bibliotecas de alto nivel como MPI [MPI94] o PVM [PVM94], y memoria compartida usando directivas de OpenMP [OMP07] [GKKG03]. En este sentido, [GBMB10] propone una estrategia para organizar el procesamiento de consultas sobre espacios métricos en nodos multi-core. Finalmente, trabajos recientes han tratado nuevas tecnologías de memoria compartida, entre las cuales se destacan plataformas basadas en GPU [DEXA12] [GDB08] [ICCSDE12] [ISCSCT09].

OpenMP es una interfaz de programación de aplicaciones (API) para la programación multiproceso de memoria compartida en múltiples plataformas. Consiste en una especificación de un conjunto de directivas de compilador, rutinas de biblioteca y variables de entorno que pueden ser usadas para paralelismo de alto nivel en programas escritos en C, C++ y Fortran sobre la base del modelo de ejecución fork-join. Está disponible en muchas arquitecturas, incluidas las plataformas de Unix y de Microsoft Windows y distribuye el procesamiento hacia los núcleos del microprocesador.

Por otro lado, las unidades de procesamiento gráfico (GPU o Graphical Process Unit) disponen de un alto número de cores con un alto ancho de banda. Este tipo de dispositivos permite aumentar la capacidad de procesamiento respecto de las CPU [FM07]. Una tendencia denominada Computación de Propósito General sobre GPU o GPGPU ha orientado la utilización de GPU sobre nuevos tipos de aplicaciones. En este sentido, las empresas fabricantes de dispositivos GPU han propuesto nuevos lenguajes o extensiones para los lenguajes de alto nivel más utilizados. Un ejemplo es [CUDA], que consiste en una plataforma software que permite utilizar las GPU para aplicaciones de propósito general, con la capacidad de manejar un gran número de hilos.

Finalmente, una aplicación construida con un modelo híbrido de programación paralela se puede ejecutar en un cluster de computadoras utilizando OpenMP y otras tecnologías como MPI y GPU, o a través de las extensiones de OpenMP para los sistemas de memoria distribuida.

Paralelismo sobre Espacios Métricos

Existe una serie de características poco comunes en las estructuras métricas que hacen difícil su implementación directa para aplicaciones reales. La primera tiene relación con capacidades dinámicas: la mayoría de estas estructuras deben ser reconstruidas si existen nuevos objetos que indexar o si hubiese que eliminar objetos de la base de datos. Otra característica, aún menos frecuente, está relacionada con estructuras que permitan la manipulación eficiente de los datos en memoria secundaria, donde deben ser considerados parámetros de costo adicional como son el número de accesos a disco y el tamaño del índice, entre otros. Finalmente, las estructuras métricas en general no consideran la jerarquía de memoria; por ello, resulta relevante considerar este aspecto para poder obtener un mayor rendimiento y eficiencia ante la posibilidad de utilizar tecnologías como las GPU, que poseen distintos niveles de memoria dentro de su sistema.

Resulta poco factible la utilización de una estructura en aplicaciones reales si ésta no considera su implementación en entornos paralelos. En la paralelización de estructuras métricas deben considerarse, entre otros aspectos, la distribución adecuada de la base de datos sobre el entorno, por ejemplo en un cluster de PCs; la paralelización de los métodos de búsqueda; eficiencia en la comunicación entre los procesadores; etc.

De acuerdo a los antecedentes disponibles y los trabajos previos realizados, se ha planteado la implementación de distintas soluciones sobre espacios de datos disímiles, tales como histogramas de colores, bases de datos de palabras, vectores de coordenadas, vectores de gauss, imágenes NASA y otros, con el fin de identificar en dichos espacios la forma óptima de distribución de los datos, tanto de la base de datos como de las estructuras, en ambientes de GPU y/o Multi-GPU, en las memorias administradas por  las CPUs y las memorias dedicadas de las GPU. Finalmente, se pretende a futuro evaluar la escalabilidad de las implementaciones de acuerdo al tamaño de la Base de Datos, y consecuentemente el almacenamiento y procesamiento de Bases de Datos y consultas en memoria secundaria. A continuación se presentan los casos de estudio, resultados y conclusiones obtenidas.

Análisis, Discusión y Resultados

La paralelización de estructuras métricas sobre GPU y en clusters de multicores son áreas de investigación poco exploradas. En este contexto, se  conocen dos grupos de investigación que están desarrollando trabajados en torno a estructuras métricas sobre plataformas basadas en GPU.  El primero de estos grupos, de la Universidad Complutense de Madrid, ha enfocado sus estudios a dos estructura métricas, la Lista de Clusters y SSS-Index, y ha presentado diversos trabajos en propuestas para kNN y consultas por rango [BGTPM11] [ISPA12]. En el segundo grupo, de la Universidad de Castilla La Mancha, participa el profesor Roberto Uribe-Paredes. Las líneas de investigación abordadas por este grupo están orientadas a desarrollar y potenciar, sobre un ambiente híbrido,  la estructura genérica presentada anteriormente [HPCS11] [ICCSDE12] [DEXA12] [JP12] [EIPA12] [WICC13]. Finalmente, en [BGTPM11] y [HPCS11] se utilizan estructuras métricas sobre una GPU y comparan sus resultados con versiones secuenciales. En [HPCS11] se utiliza una estructura métrica y se comparan los resultados obtenidos para la búsqueda por rango con versiones secuencial y multicore-CPU, mostrando una mejora notable al usar este nuevo tipo de plataforma.

Basados en las experiencias de los integrantes del grupo de investigación, se ha propuesto confirmar o refutar la hipótesis de la conveniencia de utilización de estructuras métricas genéricas basadas en pivotes en ambientes GPU. Para ello, se propone inicialmente:

• Por un lado, se pretende evaluar el rendimiento de la búsqueda sobre estructuras GMS en comparación con la búsqueda realizada por fuerza bruta.
• Por otro lado, se compara el rendimiento de la GPU frente a otras opciones de procesamiento. Se busca con ello determinar espacios y dimensiones donde es realmente conveniente utilizar estructuras métricas sobre plataformas basadas en GPU.

Para el análisis, se ha realizado un exhaustivo conjunto de pruebas de laboratorio sobre un amplio conjunto de ambientes y espacios.

Casos de Estudio

Para los experimentos llevados a cabo por el grupo de investigación, se han seleccionado distintos espacios métricos considerados representativos para este tipo de problemas. Con la finalidad de clasificar dichos espacios, se utiliza la función de distancia utilizada para la búsqueda por similitud. De esta manera, es posible identificar dos grupos de espacios métricos.

El primer conjunto de espacios corresponde a diccionarios de distintos idiomas. La función de distancia utilizada es la distancia de edición, que corresponde al mínimo número de inserciones, eliminaciones o sustituciones necesarias para que una palabra sea igual a otra. Los rangos de similitud aplicados en la búsqueda van de 1 a 4. A continuación, algunos ejemplos de la aplicación de la función de distancia:

El segundo grupo de espacios métricos contiene bases de datos de vectores de distintas dimensiones, los cuales representan distintos objetos; son predominantemente histogramas de colores de distintas imágenes (fotos de rostros, imágenes satelitales, diagramas), en donde dichos histogramas son representados en la forma de vectores de distintas dimensiones. Para este segundo grupo, se ha elegido como función de distancia la distancia Euclidiana, y se usaron rangos que recuperaban el 0.01%, 0.1% y 1% de similitud desde el conjunto de datos.

Para llevar a cabo los experimentos, ambas bases de datos se dividen en dos conjuntos aleatorios; el primero contiene el 90% de los objetos de la base, y se utiliza para construir las estructuras métricas; el 10% restante se utiliza como objetos de consulta sobre el primer conjunto. Los costes de construcción de las estructuras no son considerados en los tiempos medidos. En la Tabla 1 se presenta un resumen de las bases de datos de vectores utilizadas en los distintos experimentos. Los espacios de palabras utilizados son descritos en la Tabla 2.

Tabla 1. Espacios Métricos de Vectores utilizados en los experimentos.

Tabla 2. Espacios Métricos de Palabras utilizados en los experimentos.

Como plataforma de evaluación experimental, se ha trabajado con los espacios métricos mencionados en un entorno multicore y un entorno GPU, utilizando la estructura GMS basada en distintas cantidades de pivotes y el algoritmo de búsqueda por fuerza bruta. Para cada rutina, se ejecuta la aplicación 4 veces y se obtiene un promedio. Los experimentos generados para cada espacio métricos consisten en un producto cartesiano de las variables descritas a continuación:

• Índices / Estructuras / Algoritmo: Fuerza Bruta y GMS basada en pivotes.
• Cantidades de Pivotes utilizadas (para GMS): 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 y 1024.
• Procesadores: 1 CPU (secuencial), 4 CPU (multi-core), 8 CPU (multi-core con hyper-threading) y GPU (utilizando memoria global y memoria compartida).

Para cuantificar el universo de experimentos, se presenta a continuación en la Tabla 3 un resumen de las variables tenidas en cuenta y experimentos realizados.

Tabla 3. Resumen de los experimentos realizados.

Finalmente, el hardware utilizado corresponde a un Intel® Core™ i7-2600 CPU @3.40GHz de 4 núcleos y soporte de Hyper-Threading, 12GB de memoria principal y dos tarjetas Nvidia EVGA DDR5 de 384 cores CUDA y 1 GB de memoria global cada una. La codificación de las estructuras métricas y de los algoritmos de búsqueda se ha realizado utilizando el lenguaje C (gcc 4.3.4), ejecutadas sobre una plataforma Linux Ubuntu 12.04 LTS (Precise Pangolin); para la paralelización, se ha adoptado CUDA SDK v3.2 para el caso de las aplicaciones GPU, y se ha utilizado la librería OpenMP para la paralelización multi-CPU.

Resultados Preliminares

A continuación, se detallan los resultados de la evaluación experimental. Cabe resaltar que los experimentos fueron realizados de modo que se pudiera realizar las siguientes comparaciones:

1. Eficiencia de las distintas opciones de procesamiento. Se han realizado experimentos con códigos diseñados para el procesamiento de distintos tipos:
   • Secuencial: utilización de 1 sólo core en su capacidad máxima.
   • Multi-core: utilización de los 4 cores en su máxima capacidad con OpenMP.
   • Hyper-Threading(TM): utilización de los 4 cores en su máxima capacidad en modo Hyper-Threading con OpenMP.
   • GPU con el procesamiento en memoria global.
   • GPU con procesamiento distribuido en memoria compartida.
2. Estructura Genérica GMS vs. Algoritmo de Fuerza Bruta: por un lado, se han realizado experimentos empleando el algoritmo de Fuerza Bruta. Por otro lado, se emplearon distintas cantidades de pivotes (1, 2, 4, 8, 16, 32, 64, 128, 256, 512 y 1024) con el fin de identificar la cantidad más eficiente en cada experimento.

Los experimentos fueron realizados sobre las distintas bases especificadas en el punto anterior. A continuación, se presenta una selección de resultados relevantes que orientan el análisis de los experimentos realizados. Dicho análisis se basa en el estudio de los tiempos de procesamiento. Se utilizarán gráficos en los cuales los ejes de los gráficos corresponden al tiempo de procesamiento en segundos (Y) en los distintos rangos propuestos anteriormente (X).

Procesamiento Secuencial vs. Procesamiento Paralelo

Este primer bloque de análisis realizados contempla las distintas opciones de procesamiento (secuencial, multicore, GPU con uso de memoria global, GPU con distribución en memoria compartida),  sobre el algoritmo Fuerza Bruta; ello nos permite visualizar el rendimiento del procesamiento plano de toda la base de datos sin el uso de índices o estructuras especiales. Se han utilizado como casos de estudio los experimentos sobre un espacio métrico de vectores de dimensión absoluta 112 (Histogramas) y palabras del diccionario español. Se ha adoptado esta selección inicial a fin de exhibir de un modo general el rendimiento de las aplicaciones sobre las distintas funciones de evaluación de distancia descritas en el presente documento.

Para cuantificar los resultados, se utilizan como unidad de medida los tiempos de procesamiento en segundos. Luego, se calcula la razón entre el tiempo transcurrido entre dos resultados A y B, dando origen al speed-up de latencia. En este primer análisis, se puede constatar una diferencia significativa entre el procesamiento secuencial y las distintas opciones de procesamiento paralelo. A continuación, se pueden observar los tiempos de procesamiento obtenidos y los valores de Speedup correspondientes.

Tabla 4.  Valores de Speedup sobre una búsqueda de rango 1 en un espacio métrico de Palabras.

La mayor diferencia constatada es con el uso de la memoria compartida (GPU SM) respecto del procesamiento secuencial, que resulta en un Speedup de 60.2, 56.2, 54.21 y 52.89 para los rangos 1, 2, 3 y 4, respectivamente.

Cabe resaltar que los resultados anteriores no son suficientes para corroborar la eficiencia del procesamiento con GPU, por lo que se realizaron experimentos sobre distintos espacios métricos. Se exhiben a continuación los resultados obtenidos en experimentos realizados sobre un espacio métrico de vectores.

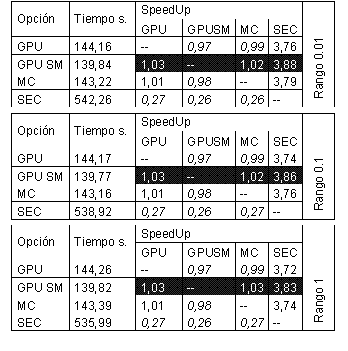Tabla 5. Speedup obtenidos en la búsqueda sobre un espacio de vectores.

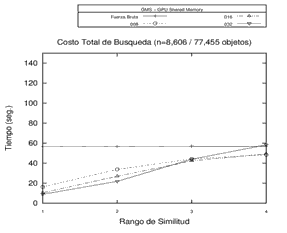
Como se puede observar, el speedup obtenido en el procesamiento de la memoria compartida en comparación con el procesamiento secuencial fueron de 3.88, 3.86 y 3.83 para los rangos de búsqueda 0.01%, 0.1% y 1%, respectivamente. En este mismo sentido, este segundo experimento presenta una mayor equidad en los tiempos de procesamiento comparado con el espacio métrico utilizado anteriormente, en lo referente al rendimiento de las distintas opciones de paralelismo. En el caso anterior, es posible apreciar valores de speedup cercanos a 11.4 (GPU con memoria compartida vs. GPU con memoria global) y 9.8 (GPU con memoria compartida vs. Multicore con Hyper-Threading). En el último ejemplo, los valores de speedup obtenidos fueron respectivamente de 1.03 / 1.02, 1.03 / 1.02 y 1.03 / 1.03. Se exhiben en la Figura 2 los tiempos obtenidos sobre un espacio métrico de palabras.

Estructuras Métricas vs. Fuerza Bruta

El análisis anterior nos ha permitido identificar que, en un entorno de procesamiento por Fuerza Bruta – es decir, sin el uso de estructuras métricas –, el procesamiento en paralelo utilizando la memoria compartida de la GPU presenta un rendimiento sustancialmente superior al procesamiento multi-core y GPU únicamente con el uso de la memoria global. No obstante, el análisis sobre estructuras métricas es más complejo y debe realizarse considerando el coste de procesamiento y almacenamiento de dichas estructuras en la jerarquía de memoria de los dispositivos, por lo que se hace necesario realizar distintas evaluaciones en cuanto al tamaño de las bases de datos y sus respectivas estructuras métricas, y su comportamiento en cuanto a distintas cantidades de pivotes y, por ende, a estructuras de distintos tamaños.

Con vistas a profundizar el estudio, se presentará el resultado de distintos experimentos que permiten dar cuenta del rendimiento de las estructuras métricas bajo las distintas técnicas de paralelismo. Para ello se han realizado experimentos utilizando estructuras con distintas cantidades de pivotes (1, 2, 4, 8, 16, 32, 64, 128, 256, 512 y 1024 pivotes) en OpenMP y GPU (memoria global y luego memoria compartida) sobre espacios métricos de distintas características en cuanto a los siguientes parámetros:

• cantidad de elementos (y el respectivo tamaño de las estructuras GMS creadas)
• tamaño de los objetos:dimensión (vectores) o largo máximo de la palabra con mayor cantidad de caracteres (palabras); y
• la función de distancia utilizada.

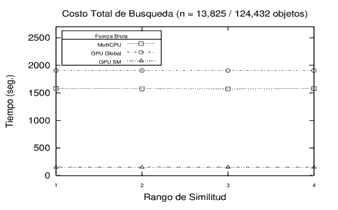
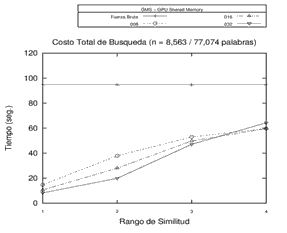
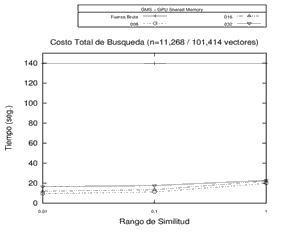
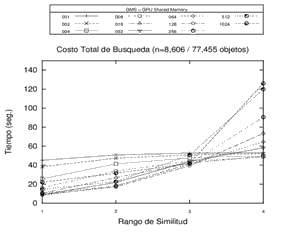
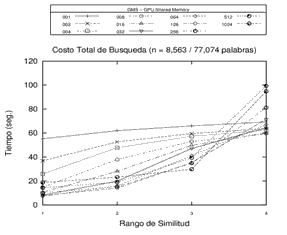
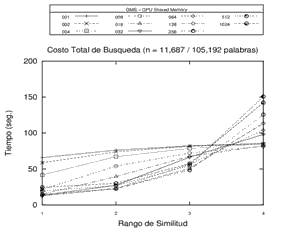
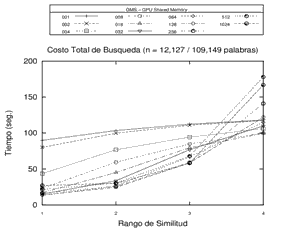
Inicialmente, se realizó el procesamiento sobre 3 espacios métricos diferentes en cuanto a la dimensión de sus objetos, la cantidad de elementos y el tipo de objeto (y su respectiva función de evaluación de distancia) utilizando la memoria compartida de la GPU. Se buscó observar el tiempo de procesamiento en fuerza bruta y sobre una estructura métrica genérica con distintas cantidades de pivotes. Los resultados obtenidos en los experimentos revelan que los tiempos de búsqueda sobre la GMS han sido predominantemente mejores que el procesamiento por Fuerza Bruta para 8, 16 y 32 pivotes. Los resultados de este experimento en particular se pueden observar en la Figura 3.

Figura 3. Resultados del Procesamiento - Fuerza Bruta y Estructura GMS con 8, 16 y 32 pivotes en distintos espacios métricos.
Cada gráfico representa un espacio métrico distinto.

Impacto del Rango de Búsqueda sobre el desempeño de Estructuras Métricas

Los experimentos realizados nos permitieron constatar una variación en los tiempos de procesamiento de acuerdo al rango de búsqueda aplicado en las rutinas que utilizan la estructura GMS, al contrario de lo que ocurre en el algoritmo de Fuerza Bruta, en el cual los tiempos de procesamiento son uniformes para los distintos rangos de búsqueda.

En este sentido, también ha sido posible constatar que el tiempo de procesamiento sobre estructuras métricas tiende a aumentar a medida que el rango de búsqueda aumenta, pues se tiende a realizar más evaluaciones de distancia a medida en que el rango de búsqueda se incrementa.

Impacto de la selección de pivotes

De acuerdo a la literatura vigente, algunos criterios para la eficiencia de las estructuras basadas en pivotes son por un lado la selección de cantidades de pivotes y, por otro lado, la elección de los pivotes. Así, se realizaron experimentos utilizando la memoria compartida de la GPU sobre estructuras métricas de 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 y 1024 pivotes, con el fin de visualizar el comportamiento de las estructuras en distintas cantidades de pivotes. Cabe resaltar que los experimentos realizados han utilizado pivotes seleccionados aleatoriamente. Asimismo, las bases utilizadas no superan la capacidad de procesamiento del hardware utilizado en cuanto al volumen de datos.

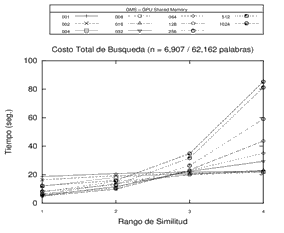
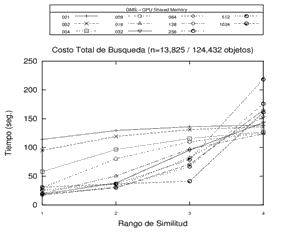
Finalmente, es posible destacar algunas conclusiones de los experimentos llevados a cabo, que permiten identificar algunas tendencias en cuanto a la cantidad de pivotes utilizados. Por un lado, se registra un decremento en el rendimiento (aumento en los tiempos) a la medida que se aumenta el rango de búsqueda en estructuras con altas cantidades de pivotes. Por otro lado, el comportamiento de las estructuras con pocos pivotes mejora (se reducen los tiempos) en la medida en que aumenta el rango de búsqueda. Es decir que, en líneas generales, sería conveniente utilizar más pivotes en los rangos de búsquedas más bajos, y adoptar estructuras con menores cantidades de pivotes en rangos de búsquedas más altos. El comportamiento observado puede visualizarse en los gráficos de la Figura 4.

Figura 4. Experimentos con estructura GMS de 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 y 1024 pivotes sobre distintos espacios métricos utilizando la memoria compartida de la GPU. Cada gráfico representa un distinto espacio métrico.

Paralelismo sobre Estructuras GMS

El último análisis propuesto en este trabajo tiene como objetivo evaluar el método de paralelismo más eficiente sobre estructuras métricas genéricas en distintos espacios métricos, de manera que se pueda constatar la conveniencia del uso de GPU con estructuras métricas. Para ello, se realizaron experimentos sobre distintos espacios métricos bajo las distintas modalidades de procesamiento paralelo descritas en este trabajo (OpenMP, GPU con memoria global y GPU con memoria compartida) y sobre distintas cantidades de pivotes.

Los resultados obtenidos nos permitieron observar dos tendencias en el comportamiento de las estructuras: por un lado, los tiempos de búsqueda con la estructura métrica genérica aumentan a medida que aumentan los rangos de búsqueda en todos los entornos de paralelismo y en cualquier cantidad de pivotes, para todos los casos. Por otro lado, es posible observar en los experimentos que el rendimiento del procesamiento con la memoria compartida de la GPU resulta conveniente a medida en que aumenta el rango de búsqueda (consecuentemente la cantidad de evaluaciones de distancia realizadas).

Excepcionalmente, se identificaron algunos casos en que el procesamiento con OpenMP ha sido más eficiente que el procesamiento con GPU: en los espacios métricos de palabras, se identificaron algunos casos particulares con el rango de búsqueda más bajo (1), como se puede observar a continuación, en las Tablas 6 y 7.

Tabla 7. Speedup obtenidos en el procesamiento de un espacio métrico sobre GPU (memoria global vs. memoria compartida).

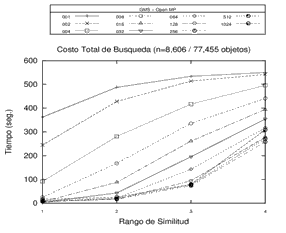
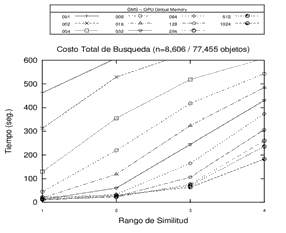
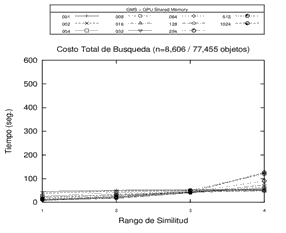
Un ejemplo de los tiempos de procesamiento obtenidos se pueden apreciar en la Figura 5.

Figura 5. Tiempos de procesamiento en Open MP, GPU memoria Global y GPU memoria compartida sobre un mismo espacio métrico con estructuras GMS de 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 y 1024. Cada gráfico corresponde a una opción de procesamiento.

Conclusiones y Trabajos Futuros

La necesidad de procesar grandes volúmenes de datos requiere de incrementar la capacidad de procesamiento y reducir los tiempos de búsqueda. En este contexto, es relevante el estudio en términos de la paralelización de los algoritmos y de la distribución de la base de datos. Por otro lado, el aumento de tamaño de las bases de datos y la aparición de nuevos tipos de datos sobre los cuales no interesa realizar búsquedas exactas, crean la necesidad de plantear nuevas estructuras para búsqueda por similitud o búsqueda aproximada.  Así también, las aplicaciones reales requieren que dichas estructuras permitan ser almacenadas en memoria secundaria eficientemente, como también que posean métodos optimizados para reducir los costos de accesos a disco.

Hemos presentado en este documento las principales características de los llamados espacios métricos y algunas estructuras métricas utilizadas para la realización de búsquedas por similitud en dichos espacios. Se ha profundizado la discusión sobre aquellos experimentos basados en la utilización de estructuras genéricas basadas en pivotes, comparados con el procesamiento linear o secuencial conocido como procesamiento por fuerza bruta. Por otro lado, hemos presentado los resultados de experimentos utilizando distintas estrategias de procesamiento paralelo, analizando el rendimiento de la búsqueda en ambientes con GPU (CUDA) y multi-core (OpenMP). Con base en el marco teórico vigente y en los experimentos realizados, es posible arribar a distintas conclusiones, resumidas a continuación.

• Las distintas tecnologías de procesamiento paralelo utilizadas permiten lograr una optimización en los tiempos de procesamiento comparadas con el procesamiento secuencial, registrando distintos coeficientes de speedup. En un análisis más detallado, es posible finalmente observar en líneas generales un grado de optimización en el rendimiento cuando se utiliza el procesamiento basado en la memoria compartida de la GPU en relación a las demás opciones utilizadas, excepto en algunas implementaciones de la estructura métrica basada en pivotes en los que el rango de búsqueda es bajo y por ende no se realizan muchas operaciones de evaluación de distancia. Por otro lado, el rango de búsqueda no es un factor determinante en el rendimiento de las aplicaciones en el algoritmo de fuerza bruta. Bajo este algoritmo, la utilización de la memoria compartida de la GPU se ha mostrado más eficiente que las demás modalidades de paralelismo en todos los casos registrados.
• Para la mayoría de los experimentos, la utilización de estructuras métricas basadas en una cantidad moderada de pivotes ha permitido obtener tiempos de procesamiento inferiores al uso del algoritmo de Fuerza Bruta. Se ha corroborado que los tiempos de búsqueda con la estructura métrica genérica aumentan a medida que aumentan los rangos de búsqueda en todos los entornos de paralelismo y en cualquier cantidad de pivotes, para todos los casos. El procesamiento con GPU resulta más eficiente a medida en que aumenta el rango de búsqueda - y consecuentemente la cantidad de evaluaciones de distancia realizadas -.
• Por otro lado, se identificaron algunas tendencias en cuanto al impacto de la cantidad de pivotes utilizados sobre la estructura métrica genérica: mientras se registra un aumento en los tiempos a medida que se aumenta el rango de búsqueda en estructuras con altas cantidades de pivotes, el comportamiento de las estructuras con pocos pivotes presenta mejores tiempos de procesamiento a medida que aumenta el rango de búsqueda.

Como trabajo futuro se propone discutir la escalabilidad del uso de esas plataformas, ya que actualmente se proponen experimentos en equipos individuales. Se propone llegar a soluciones híbridas que permitan la distribución de los espacios métricos y sus correspondientes estructuras, de modo que sea posible realizar aplicaciones sobre volúmenes de datos en escala de producción.

Por último, otra línea de gran interés a ser abordada está relacionada con la eficiencia energética en el uso de distintos dispositivos y tecnologías para el procesamiento paralelo de grandes volúmenes de información en lo referido a la búsqueda por similitud sobre espacios métricos.

Bibliografía - Bibliography

[CUDA] NVIDIA CUDA C Programming Guide, V. 4.0.

[CPM94] R. BAEZA-YATES, W. CUNTO, U. MANBER, and S. Wu. Proximity matching using fixed queries trees. In 5th Combinatorial Pattern Matching (CPM’94), 1994, LNCS 807, pp. 198–212.

[DEXA12] Roberto Uribe-Paredes, Enrique Arias, José L. Sánchez, and Diego Cazorla. Improving the Performance for the Range Search on Metric Spaces using a Multi-GPU Platform. To appear: 23rd International Conference on Database and Expert Systems Applications (DEXA 2012). Vienna, Austria, Sept. 2012.

[EIPA12] Osiris SOFIA, Jacobo SALVADOR, Eder DOS SANTOS, Roberto URIBE PAREDES. Búsquedas por Similitud en Espacios Métricos sobre Plataformas Basadas en GPUs. II Encuentro de Investigadores de la Patagonia Austral, Universidad Nacional de la Patagonia Austral, Unidad Académica San Julián, Puerto San Julián, Argentina. 7 de septiembre de 2012. Proceeding Publicados en CD por Universidad Nacional de la Patagonia Austral.ISBN13: 978-987-1242-66-5.

[FM07] Wu-Feng and Dinesh Manocha. High-performance computing using accelerators. Parallel Computing, 33:645--647, 2007.

[GBMB10] Veronica Gil-Costa, Ricardo Barrientos, Mauricio Marín, and Carolina Bonacic. Scheduling metric-space queries processing on multi-core processors. Euromicro Conference on Parallel, Distributed, and Network-Based Processing, 0:187--194, 2010.

[GDB08] Vincent Garcia, Eric Debreuve, and Michel Barlaud. Fast k nearest neighbor search using GPU. Computer Vision and Pattern Recognition Workshop, 0:1--6, 2008.

[GKKG03] GRAMA, Ananth and KARYPIS, George and KUMAR, Vipin and GUPTA, Anshul. Introduction to Parallel Computing (2nd Edition). Addison Wesley. 2003.

[HPCS11] Roberto URIBE-PAREDES, Pedro VALERO-LARA, Enrique ARIAS, José L. SÁNCHEZ and Diego CAZORLA. Similarity search implementations for multi-core and many-core processors. In: 2011 International Conference on High Performance Computing and Simulation (HPCS), pp. 656–663 (July 2011). Istanbul, Turkey.

[ICCSDE12] Roberto Uribe-Paredes, Diego Cazorla, José L. Sánchez, and Enrique Arias. A comparative study of different metric structures: Thinking on gpu implementations. In International Conference of Computational Statistics and Data Engineering (ICCSDE’12), London, England, July 2012.

[ISCSCT09] Quansheng Kuang and Lei Zhao. A practical GPU based kNN algorithm. International Symposium on Computer Science and Computational Technology (ISCSCT), pp. 151–155, 2009.

[ISPA12] R.J. Barrientos, J.I. Gómez, C. Tenllado, M. Prieto, and M. Marin. Range query processing in a multi-GPU enviroment. In 10th IEEE International Symposium on Parallel and Distributed Processing with Applications (ISPA 2012), Madrid, Spain, July 2012.

[JISBD12] E. ARIAS, D. CAZORLA, J. L. SÁNCHEZ, R. URIBE-PAREDES. Una estructura Métrica Genérica para Búsquedas por Rango sobre una Plataforma Multi-GPU. XVII Jornadas de Ingeniería del Software y Bases de Datos (JISBD2012). Sept. 2012, Almería, España.

[JP12] Roberto Uribe-Paredes, Diego Cazorla, Enrique Arias and José L. Sánchez. Acelerando la Búsqueda por Rango con un Sistema Híbrido de Memoria Compartida. To appear: Actas XXIII Jornadas de Paralelismo (JP2012). Sept. 2012, Elche, España.

[MOV94] María Luisa MICÓ, José ONCINA, and Enrique VIDAL. A new version of the nearest-neighbour approximating and eliminating search algorithm (AESA) with linear preprocessing time and memory requirements. Pattern Recognition Letters, 15(1):9--17, January 1994.

[MPI94] W. Gropp, E. Lusk, and A. Skelljum. Using MPI: Portable Parallel Programming with the Message Passing Interface. Scientific and Engineering computation Series. MIT Press, Cambridge, MA, 1994.

[NN97] S. Nene and S. Nayar. A simple algorithm for nearest neighbor search in high dimensions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 19(9):989--1003, 1997.

[OMP07] Barbara Chapman, Gabriele Jost, and Ruud van der Pas. Using OpenMP: Portable Shared Memory Parallel Programming. The MIT Press, 2007.

[SOFSEM07] Oscar Pedreira and Nieves R. Brisaboa. Spatial selection of sparse pivots for similarity search in metric spaces. In 33rd Conference on Current Trends in Theory and Practice of Computer Science (SOFSEM 2007), Harrachov, Czech Republic, 2007, vol. 4362 of LNCS, pp. 434–445, Springer.

[SPIRE99] Edgar CHÁVEZ, José L. MARROQUÍN, and Ricardo BAEZA-YATES. Spaghettis: An array based algorithm for similarity queries in metric spaces. In 6th International Symposium on String Processing and Information Retrieval (SPIRE 99), pages 38--46. IEEE CS Press, 1999.

[TTSF00] Caetano Traina, Agma Traina, Bernhard Seeger, and Christos Faloutsos. Slim-trees: High performance metric trees minimizing overlap between nodes. In VII International Conference on Extending Database Technology, pages 51--61, 2000.

[VLDB95] Sergei Brin. Near neighbor search in large metric spaces. In the 21st VLDB Conference, pages 574—584. Morgan Kaufmann Publishers, 1995.

[VLDB97] Paolo Ciaccia, Marco Patella, and Pavel Zezula. M-Tree : An efficient access method for similarity search in metric spaces. In the 23st International Conference on VLDB, pages 426--435, 1997.

[VLDBJ02] Gonzalo Navarro. Searching in metric spaces by spatial approximation. The Very Large Databases Journal (VLDBJ), 11(1):28--46, 2002.

[WICC13] Osiris SOFIA, Jacobo SALVADOR, Eder DOS SANTOS, Roberto URIBE PAREDES. Búsquedas por Rango sobre Plataformas GPU en Espacios Métricos. pp 658 - 662. XV Workshop de Investigadores en Ciencias de la Computación - WICC 2013. 18 al 18 de Abril de 2013. Universidad Autónoma de Entre Ríos, Paraná, Argentina. Proceeding Publicados en CD por Universidad Autónoma de Entre Ríos y RedUNCI. ISBN13: 978-987-28179-6-1.

Google Scholar Index

Article

Evaluación de estructuras métricas con Unidades de Procesamiento Gráfico de Propósito General

Publisher:

Ciencia y Técnica Administrativa - CyTA