Research article

Medición de rendimiento del algoritmo spmv utilizando contadores de hardware para GP GPU en arquitecturas no homogéneas

Resumen

En la presente investigación se busca analizar diferentes contadores de hardware durante la ejecución del algoritmo SPMV (multiplicación vector por matriz dispersa), a través del uso de herramientas de profiling utilizadas en placas gráficas de los fabricantes ATI y NVIDIA. Utilizando como base tres bibliotecas que hacen uso del procesador gráfico, se busca inferir a partir del estudio de los diferentes indicadores, las optimizaciones aplicables en el contexto planteado que mejoren el desempeño. Para analizar los resultados, se propuso una división de los tres principales eventos de la arquitectura (escritura, ejecución y lectura). Se trabajó en el análisis de las notorias diferencias detectadas en los tiempos de respuestas debido al volumen de las transferencias de datos, para luego analizar la implementación de una biblioteca en particular para cada arquitectura hardware. Finalmente se propone una pequeña modificación que logra mejorar el rendimiento de ambas arquitecturas.

Abstract

Palabras Clave:

GPU, CUDA, OpenCL ⓘ

Keyword:

Contadores de hardware, , ⓘ

1. Introducción

En una gran cantidad de aplicaciones científicas actuales, una de las operaciones algebraicas más utilizadas, es la operación Matriz x Vector. Esta misma esta implementada en diversas bibliotecas de análisis numérico, entre ellas, la reconocida biblioteca BLAS (Blas, 2015).

Cuando la matriz con la que se desea operar, tiene características de ser una matriz dispersa, existen diversos métodos para optimizar el almacenamiento y procesamiento de esta matriz. Debido a la naturaleza de esta matriz (Posee una gran cantidad de elementos de valor iguales a cero), las optimizaciones de almacenamiento aprovechan este conocimiento a priori, para reducir el espacio que ocupa esta matriz en memoria, como así también para realizar las operaciones matemáticas de forma diferente.

Cuando se recurre a una implementación de la operación matriz x vector, es común encontrar algoritmos paralelos que resuelvan el problema, debido a sus propiedades de independencia de datos y operaciones. Esta misma característica, es la que habilita el uso de procesadores escalares masivos para resolver la lógica algebraica necesaria.

Teniendo en cuenta, que el procesador gráfico (GPU), es hoy en día, el procesador escalar más comúnmente utilizado en el ámbito científico para la resolución de problemas masivamente paralelos, las bibliotecas estándar para resolución de la operación matriz x vector para matrices dispersas, se encuentran implementadas para las dos tecnologías más utilizadas: OpenCL (Khronos, 2015) y CUDA (Nvidia, 2015). En la actualidad los principales fabricantes, son dos. La empresa ATI (R), adoptó la biblioteca de código abierto llamada  OpenCL. Por otro lado NVIDIA(R), desarrollo su propia biblioteca de trabajo llamada CUDA, soportando además OpenCL.

Los problemas que involucran la utilización de matrices dispersas, requieren un tratamiento diferente a los problemas de matrices convencionales. El objetivo del presente trabajo es realizar una comparación de rendimiento entre distintas implementaciones que intentan optimizar este tipo de matrices, comparando la ejecución en hardware que utiliza el procesamiento general utilizando procesadores gráficos (GP-GPU, de sus siglas en inglés).

2 Desarrollo del trabajo

2.1 Matrices dispersas

Se está ante una matriz dispersa o rala cuando la densidad de elementos, con valor significativo distinto de cero (EDC), es muy pequeña (De Luca 2015).

Para este tipo de matrices utilizar el formato de representación denso lo hace muy costoso tanto en recursos de almacenamiento como tiempo de procesamiento. Ya que se almacenan elementos y se los utilizan en operaciones que no influyen en el resultado final del algoritmo.
Por ese motivo existen distintos formatos de representación de las matrices dispersas (tales como COO, CRS, CCS, ELL, ELLP, DIA, entre otros (Neelima & Raghavendra, 2012). La diferencia de estos formatos radica en que deben indicar explícitamente la posición de los EDC, mientras que en el formato denso, es conocido por su ubicación.

Los formatos utilizados en la presente investigación son COO, CRS y MM.

• COO: Es el formato más simple, posee las coordenadas (fila y columna) para los EDC. Suele utilizarse como almacenamiento y no en cálculos (Fig. 1 A).
• CRS: Contiene similar información que el formato COO, pero su diferencia radica en que las filas son representadas como índices a los valores de datos que la forman. Al tener indexada las filas puede a ahorrar espacio, evitando valores repetidos del mismo número de fila. Además al ser indexado puede conocerse en inicio y fin de una fila en los vectores de los valores y columnas (Fig. 1 B).

Fig. 1: Matriz dispersa; (A) su representación en formato COO; (B) su representación en formato CRS.

Existen formatos de almacenamiento en medios físicos ideados para matrices dispersas. El formato elegido en la investigación es de Matrix Market (Market, 2013) (MM), debido a que es soportado por la mayoría de las bibliotecas utilizadas, existen otros como MatFile (Matlab, 2015) y  Rutherford/Boeing (Duff et al, 1997), entre otros.

El archivo MM, es el utilizado para realizar la carga de las matrices. Está compuesto por dos secciones, una de cabecera y otra de contenido, la primera especifica el tipo de dato de la matriz, la cantidad de filas, de columnas y el total de EDC. El resto del archivo tiene los datos de cada EDC en forma ascendente, en formato COO (la fila, columna y valor).

2.2 Bibliotecas BLAS

Las ecuaciones que utilizan las matrices y/o vectores se engloban bajo conjunto de subrutinas básicas para álgebra lineal BLAS (“Basic Linear Algebra Subprogram”). La que define un grupo de funciones con el fin de realizar operaciones comunes sobre tipos de datos escalares, vectores y matrices.

Estas se dividen en tres niveles dados por la complejidad computacional. Los algoritmos de nivel 1 tienen un tiempo de respuesta lineal (O) (por ejemplo suma de vectores). Para el nivel 2 la respuesta es cuadrática (O2) como la multiplicación de matriz por vector. En el nivel 3 es cúbico (O3) como la multiplicación de matrices.

Existen trabajos de investigación sobre bibliotecas BLAS que con el fin de optimizar  subrutinas según características:

1. HARDWARE: como, por ejemplo, un uso óptimo de memoria cache (Haque, 2002).
2. SOFTWARE:con formatos de representación (Golub & Van Loan, 2013).

El trabajo de Liu y Vinter (Liu & Vinter, 2014) compara el algoritmo propio de multiplicación de matrices en ambas arquitecturas, la diferencia radica que el hardware utilizado posee diferentes características influyendo esto en los resultados. Mientras que  Geir Josten Lien (Lien, 2012) utiliza solo la biblioteca ViennaCL y la compara en distintas arquitecturas y sistemas operativos, sin lograr profundizar en otras bibliotecas.

En la actualidad existen diversas bibliotecas que implementan BLAS en forma paralela. Las elegimos para realizar las mediciones de rendimiento son las siguientes:

• PARALUTION: Se utilizó la versión 1 publicada en 2015 (Paralution, 2015). Brinda interfaz de objetos (C++). Soporta CPU como GPU (OpenCL y CUDA) con manejo de matrices en formato MM, cálculos en los distintos niveles de BLAS y ecuaciones de aproximación de resoluciones por métodos  interactivos y precondiciones.
• VIENNACL: Se utilizó la versión 1.6.2 disponible desde diciembre 2015 (ViennaCL, 2015). Utilizando como base la biblioteca estándar C++ de boost (Boost, 2015). Da soporte para CPU y GPU soportando CUDA, OpenCL, y OpenMP; Brindando funciones en los 3 niveles de las bibliotecas BLAS y de resoluciones por métodos interactivos.
• MAGMA: Se utilizó la versión 1.6.2 que incluye el paquete “Sparse-Iter” (Magma, 2014) que da soporte al manejo de matrices dispersas en GPU para CUDA. La biblioteca trae funciones de lenguaje C que permite leer matrices en formato MM, posee un gran manejo sobre formatos de representación de matrices dispersa con soporte a los distintos algoritmos, simplicidad de manejo de transferencia entre CPU y GPU.

2.3 Preparativos de pruebas

La finalidad de las distintas pruebas es tomar indicadores desde el profiler (medidor de rendimiento), comparando los eventos y contadores de hardware en cada GPU.

En cuanto al funcionamiento de las bibliotecas BLAS descritas existen ciertas limitaciones.

Para la biblioteca ViennaCL en ATI el uso del profiler fue exitoso. Este no fue el caso en NVIDIA, la versión del profiler no detecta actividad para OpenCL, porque no está implementado para esta tecnología, con lo cual, no pudo ser utilizado, la biblioteca Magma, en su implementación para OpenCL solo soporta matrices densas, a diferencia de la versión CUDA quesí  soporta matrices dispersas, mientras que la única biblioteca que funcionó en ambas arquitecturas fue Paralution.

2.3.1 Matrices dispersas utilizadas

Las matrices utilizadas están almacenadas en formato de MM y son del repositorio de  la Universidad de Florida (Cise, 2015). Con el fin de lograr obtener datos comparativos las matrices son del mismo tipo “real” y procesado en punto flotante con doble precisión.

Al estar almacenadas en formato COO previamente serán convertidas al formato CRS antes de ser utilizada por el algoritmo que hará la multiplicación de matriz por vector SPMV (Sparse Product Matrix Vector). La elección se debe a su importancia (Kaltofen, 2014) siendo parte central de otros, como el cálculo de gradiente conjugado.

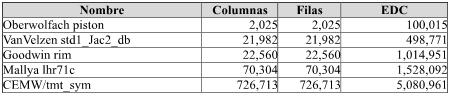
La comparación y elección de matrices está dada por la cantidad de EDC, ya que es lo que da la característica en cuanto a transferencias y cálculos de la matriz. La siguiente tabla detalla matrices elegidas:

Tabla 1: Características de matrices utilizadas.

2.3.2 Equipo de laboratorio

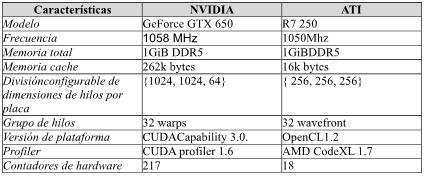
Para realizar las mediciones de rendimiento, se utilizaron dos GPUs de distinto fabricante con similares características. Las computadoras donde residen, son de idénticas características con Sistema Operativo Ubuntu 14.04 ejecutando sobre procesador Intel i5-3330 con 8 GiB de memoria RAM, la siguiente tabla muestra las características principales de las dos placas GPUs:

Tabla 2: Características de procesadores gráficos utilizadas.

Las pruebas consistieron en ejecutar el algoritmo SPMV para las matrices, arriba indicadas. De manera iterativa se realizaron diez ejecuciones por vez, desde las herramientas de profiler de cada GPU en ambos equipos.

2.4 Análisis de los resultados

Para comenzar a evaluar las bibliotecas BLAS se analizó el desempeño con la medición de tiempo de los tres principales eventos que tiene el uso de GPUs. Para lograr la comparación utilizamos una nomenclatura genérica debido a las diferencias entre fabricantes.

1. Escritura GPU: Son los eventos de transferencia de datos del CPU al GPU.
2. Kernel: Representa a los tiempos consumidos por el algoritmo SPMV en todos los hilos con la ejecución de los kernel en GPU.
3. Lectura GPU: Son todos los eventos que representan a la transferencia de datos del GPU al CPU.

La diferencia de información de los profiler requirió de la construcción de un software que nivele las mediciones. Como por ejemplo NVIDIA las mediciones de tiempos son del orden de en nano segundos. Mientras que para ATI son en ciclos de reloj, que convierten en unidades de tiempo. Para luego, a ambas mediciones, se las expresa en milisegundos con el fin de poder compararlas.

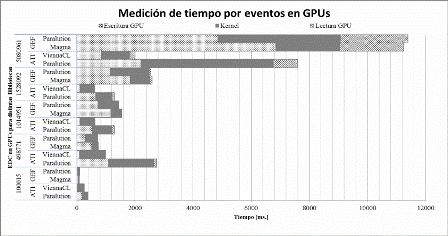
Analizando las mediciones (Fig. 2) connota que los tiempos del mismo evento para distinta biblioteca son muy distintos. Teniendo en cuenta que se utilizan las mismas matrices, la misma representación CRS y el mismo algoritmo en las bibliotecas. Con estas condiciones los tiempos de los eventos escritura y lectura deberían ser homogéneos y no lo son. Los factores que intervienen en las transferencias de datos entre CPU y GPU son fijos e independientes a las bibliotecas utilizadas. Si hay diferencia de tiempos en los eventos es porque las bibliotecas difieren en la forma de transferir. Los casos significativos en la escritura GPU, para ViennaCL donde es muy inferior, y para Magma un poco superiores al resto.

Fig. 2: Mediciones de 3 bibliotecas BLAS que utilizan las GPUs ATI y NVIDIA (GEF), indicando la cantidad EDC por cada fila y la matriz utilizada en cada prueba.

Para hallar estas diferencias por profiling discriminamos la cantidad de bytes transferidos (escritos y leídos) entre CPU y GPU. Al que se comparó con un valor de referencia mínimo teórico compuesto por los tamaños de datos de entrada y salida del algoritmo SPMV.

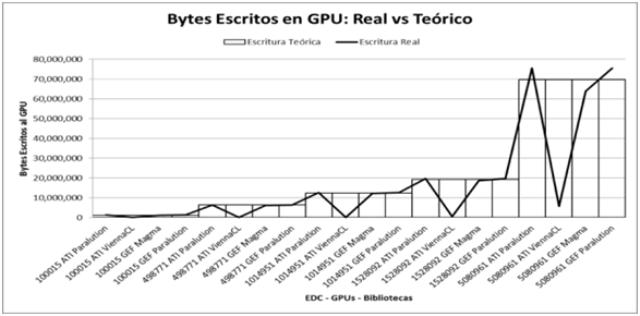
Es valor de referencia se construye en el evento escritura de GPU por la matriz de entrada que es representa en CRS. Esto implica que está formada por 3 vectores uno con los números de columnas, el otro con los EDC y de índices a filas. El tamaño de los dos primeros es la cantidad de EDC mientras que el tercer vector es la cantidad de filas más uno. También como entrada se encuentra el vector con al cual se multiplicara. Otro detalle a tener en cuenta es el tipo de dato de los vectores. Tanto el vector de la multiplicación como el vector de EDC están en doble precisión. Los vectores de columnas e  índices a fila son enteros.  (Fig. 3).

Fig. 3: Mediciones de bytes escritos a GPU por las bibliotecas BLAS.

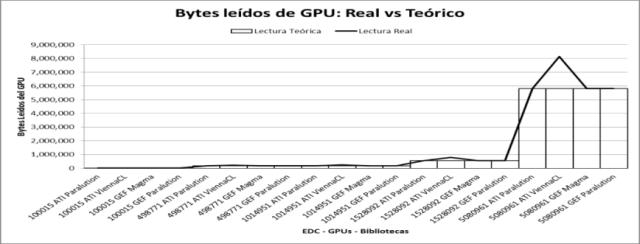
Mientras que el valor de referencia para el evento lectura GPU (Fig. 4) es formado por el vector de salida del algoritmo SPMV. Su tamaño está dado por la cantidad de filas que posea la matriz, y su tipo de dato es de doble precisión.

Fig. 4: Mediciones de bytes leídos de GPU por las bibliotecas BLAS.

Con las comparaciones  se verifica que para ViennaCL las mediciones de transferencias escritura son muy inferiores y un poco superiores en la lectura. Este resultado refleja que internamente, esta biblioteca no utiliza el formato CRS, pudiendo utilizar otro formato (por ej. ELL).

Para el caso de Magma, esta transfiere volúmenes similares al teórico, comparándola con Paralution los tiempos son superiores.

También se comprueba que Paralution tiene transferencias de escritura un poco superiores a las teóricas. Gracias a la contabilización de bytes transferidos se verifica que también transfiere el vector del resultado antes del algoritmo (en el evento escritura GPU).

2.5. Optimización de algoritmo SPMV

Debido a que la  biblioteca Paralution es la que funciona correctamente tanto en OpenCL como CUDA, llevamos a fondo el análisis de mediciones aislando solo la ejecución del hilo kernel GPU para SPMV.

Comparando el código OpenCL y CUDA detectamos que a pesar de ser de la misma biblioteca tiene distinta estructura de programación, independientemente del lenguaje escrito:

• Para OpenCL: Tiene como desventaja el uso de variables globales para definir el valor inicial y final de un ciclo. Como ventaja utiliza una variable interna para hacer multiplicaciones parciales y por último actualizar la variable global (lenta).
• Para CUDA: Se puede apreciar como desventaja que utiliza la variable global (lenta) para hacer cuentas intermedias en el ciclo principal. Como ventaja utiliza la notación del operando suma/asignación (+=) en forma óptima.

Basándonos en lo analizado anteriormente y nuestra experiencia realizamos las modificaciones a los hilos kernels GPU de SPMV, utilizando el siguiente pseudocódigo:

Entero ai = indiceDimensiones();
Real sumar = (Real) 0.0;
Entero cntMin = vMatrizAIndiceFila[ai];
Entero cntMax= vMatrizAIndiceFila[ai+1];

for( Entero aj=cntMin;aj<cntMax;aj++) {
   sumar = sumar + ( vMatrizAValor[aj] * vVectorB[vMatrizCol[aj]] );
}
vVectorR[ai] = sumar;

 

Con estructura de codificación similar a la mostrada, sin modificar la forma en que la biblioteca calcula las dimensiones, volvimos a ejecutar los profilers. El resultado se encuentra en la (Fig. 5 y Fig 6.)

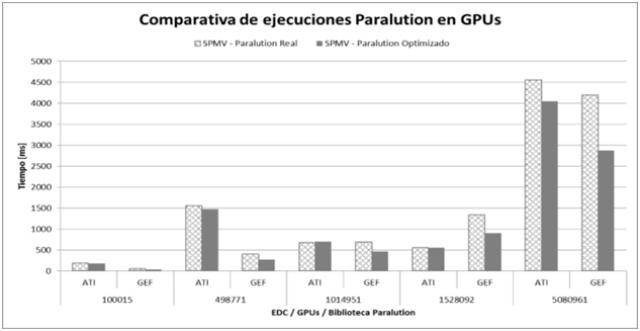
En la placa del fabricante ATI, utilizado OpenCL, el algoritmo optimizado logra una mejora del 4,4% con matrices pequeñas y cuando llega a la matriz mayor, el tiempo mejora en un 11%. En el caso de NVIDIA con el algoritmo optimizado la mejora es del 31,8% al 32,9% para las distintas matrices.

Fig. 5: Comparativa de ejecuciones SPMV de Paralution con y sin optimización en  GPUs ATI y NVIDIA(GEF).

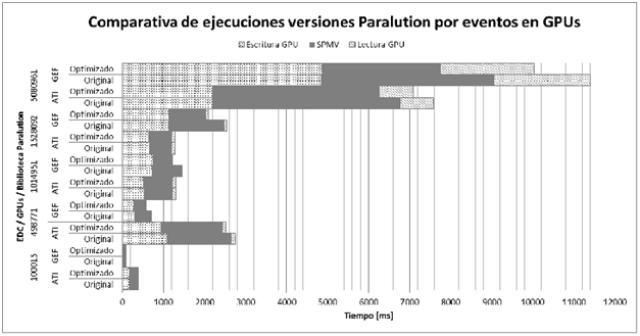
Fig. 6: Comparativa de eventos en ejecuciones SPMV de Paralution con y sin optimización para GPUs ATI y NVIDIA(GEF).

3. Conclusión

Se analizaron las bibliotecas BLAS (Magma, Paralution y ViennaCL) que utilizan GPU como soporte en la resolución de algoritmos de alto desempeño. Todas con la misma operación de SPMV (nivel 2 de BLAS) 

Utilizando dos GPUs de distintos fabricantes con similares características, se ejecutaron pruebas con sus respectivos profiler, y se desarrolló un software con el fin de normalizar los resultados.

Las pruebas consistieron en ejecutar repetidas veces, para obtener un promedio, en la medición del tiempo para tres de los principales eventos al trabajar con GPU, definiendo 3 parámetros: escritura, lectura y kernel.

Al detectar diferencias en los tiempos de respuestas de las bibliotecas en las mediciones de transferencia. Se comparan los bytes transferidos, tanto de lectura como escritura, y se los compara con valores teóricos que utiliza el algoritmo SPMV al tratar con matrices en formato CRS. Hallándose que ViennaCL internamente utiliza un formato de representación distinto, que optimiza la transferencia. También se verifica que la biblioteca Paralution transfiere un vector de más, el del resultado.

Por antes dicho, descartó en las comparaciones a ViennaCL. Ya que al cambiar la representación de la matriz, varia el tiempo de ejecución por el uso de recursos y los accesos a memoria global (que es lenta).

Enfocando el análisis en la biblioteca Paralution (la única que funciona según lo esperado en los dos GPUs) se analizó el estilo de codificación del hilo kernel y comoestá desarrollado. Se incluyeron  modificaciones con el fin de optimizarlos y los ejecutamos en ambas GPU.
Las modificaciones incluyeron minimizar el acceso a memoria global (catalogada lenta), con el uso de auxiliares en memoria interna (de rápido acceso, pero con escasa reserva). Otro de los cambios fue la utilización del operador suma/asignación en forma óptima.

Se repitió el procedimiento de pruebas ejecutando el algoritmo SPMV modificado en ambas GPUs evaluando el impacto final de los mismos. Los resultados de estas pruebas dieron que la mejora en Nvidia fue del 31,8% al 32,9%. Mientras que en ATI hubo una mejora solo del 4,4% al 11%.  Los resultados en las optimizaciones deberían impactar en forma distinta según la dispersividad de las matrices utilizadas. En ATI son muy notorias. Mientras que para NVIDIA, la diferencia es menor. Esta diferencia se debe a  la forma en que cada tecnología provee el acceso a memoria de los datos.

En la comparativa solo se pudieron utilizar algunos contadores de hardware y eventos. Sin lograr profundizar en la comparación entre los profilers. Ya que cada fabricante se enfoca en brindar la información según su criterio.

Bibliografía - Bibliography

Blas, 2015. BLAS (Basic Linear Algebra Subprograms)

Boost, 2015. Biblioteca Boost lenguaje C++

Cise, 2015. Repositorio de Matrices Dispersas

De Luca et al, 2015. Análisis de rendimiento de algoritmos de resolución de problemas de matrices dispersas para GP-GPU Computing mediante el uso de profiling de hardware. Universidad Nacional de la Matanza, WICC 2015, pp2-3.

Duff et al, 1997. The Rutherford-Boening Sparse Matrix Collection. Atlas Centre, Departament for Computation and Information, pp19-29.

Golub y Van Loan, 2013. Matrix computation. The Johns Hopkins University, Fourth Edition, pp 33-42.

Khronos, 2015. OpenCL: Spec, OpenCL 1.2 API and C Language Specification. Khronos OpenCL Working Group,Document Revision: 19, pp 22-30. 

Haque, 2002. A Computational Study Of Sparse Matrix Storage Schemes. Bachelor of Science, Islamic University of Technology, pp. 197–204.

Kaltofen, 2014. The Seven Dwarfs of Symbolic Computation. Dept. of Mathematics, North Carolina State University, pp 2,3.

Lien, 2012. Auto-tunable GPU BLAS. Norwegian University of Science and Technology, Department of Computer and Information Science, pp 6-22.

Liu y Vinter, 2014. An Efficient GPU General Sparse Matrix-Matrix Multiplication for Irregular Data. IEEE 28th International Parallel y Distributed Processing Symposium, pp 370-381.

Neelima y Raghavendra, 2012. Effective Sparse Matrix Representation for the GPU Architectures. National Institute of Technology, Karnataka, pp 3-6.

Magma, 2014. Biblioteca BLAS Magma

Market, 2013. Formato Matrix Market

Matlab, 2015. Formato Matlab

Nvidia, 2015. “CUDA™ C Programming Guide version 5.0”: NVIDIA Corporation, pp 7-80.

Paralution, 2015. Biblioteca BLAS Paralution

ViennaCL, 2015. Biblioteca BLAS ViennaCL

Google Scholar Index

Article

Medición de rendimiento del algoritmo spmv utilizando contadores de hardware para GP GPU en arquitecturas no homogéneas

Publisher:

Ciencia y Técnica Administrativa - CyTA