 |
| Figura 47 Tabla de sensibilidad de 1 variable |
Uno de los beneficios de las hojas de cálculo, consiste en la aplicación de sus herramientas que permiten realizar análisis de hipótesis de forma rápida y fácil, en las que se pueden cambiar variables decisorias y ver inmediatamente sus efectos. En este capítulo se presentan distintas opciones que permitan desarrollar las hipótesis.
Una tabla de sensibilidad es aquella que, como su nombre lo indica, produce resultados ante una o dos variables sensibles de un cálculo.
Trataremos el tema con un ejemplo, a efectos de explicar su operatividad
Supongamos que se está considerando la compra de una casa con una hipoteca de 200.000 USD a un plazo de 30 años, y se precisa calcular la cuota mensual con distintas tasas de interés. La información que se necesita se puede obtener una tabla con una variable.
Se elabora una hoja con los valores que se desean comprobar, es decir la tasa de interés
1.
a) Introducir los valores de tasas Nominales mes-vencido en el rango B3:B8
6% - 6.5% - 7% - 7.5% - 8 - 8.5%
b) Ingresar el Monto del Préstamo en la celda F1
c) Ingresar la cantidad de años en la celda F2
2 En la celda C2, se escribe la fórmula para la variable de entrada:
=PAGO(A2/12;f2*12;-F1)
A2/12: tasa mensual de interés
F2*12: duración del préstamo en meses
-F1: capital solicitado
3 La celda A2, permanece en blanco, este valor por defecto es cero
se puede observar el esquema en la Figura 47
 |
| Figura 47 Tabla de sensibilidad de 1 variable |
· Lo que se pretende con una tabla de sensibilidad, es hacer extensiva la fórmula hacia todas las tasas, pero sin necesidad de copiar la fórmula. A esta opción se tiene acceso desde la barra del menú tal como se indica en la Figura 48
 |
| Figura 48 Definición de la tabla de sensibilidad |
Seleccionar el rango de la tabla (el bloque rectangular mas pequeño que contiene la fórmula y todos los valores del rango de entrada), en este caso B2:C8. Y ahora se selecciona del menú-Datos, la opción Tabla
Como se puede observar, los valores de las diferentes tasas se colocaron en forma de columna, y así mismo en la fórmula de Pago, la tasa fue direccionada a una celda en blanco al lado de la columna de valores. Esta celda en blanco es la celda de la variable sensible. Para construir la tabla de sensibilidad debe indicarse la celda sensible, en este caso CELDA de ENTRADA (columna) (Figura 49)
 |
 |
|
| Figura 49 Definición de variables de sensibilidad | ||
Con esto los resultados son:

Si los valores de entrada se hubieran presentado en forma de fila, se debe indicar la CELDA de ENTRADA fila, tal como se presenta en la Figura 50
 |
| Figura 50 Tabla de sensibilidad, entrada fila |
Suponga en el ejemplo anterior, que se tiene otra casa vista con una hipoteca de 180000 USD.
Para llegar al resultado que se aprecia en la siguiente figura se procede de la forma como se indica en Figura 51
 |
| Figura 51 Tabla sensible con mas de una fórmula |
· En la celda D3, se introduce una nueva fórmula: =PAGO(A3/12;f3*12;g2). Tal como en el ejemplo anterior, la fórmula hace referencia a la celda A2
· Seleccionar el rango de la tabla (B3:D9)
· Con la opción Tabla del menú de datos se trabaja igual que el ejemplo anterior, haciendo referencia a la celda de entrada A2, en el cuadro de edición Celda de Entrada (columna)
· Igual que antes, cada celda del Rango C3:D8 contiene la fórmula {=TABLA(;A3)}
Las tablas de sensibilidad permiten operar con dos variables sobre una misma fórmula.
Basados en el ejemplo inicial, pero variando el tiempo para el pago de la casa en 15, 20, 25 y 30 años.
Debe construirse entonces una tabla con la información de interés y tiempo, y en la definición de las celdas de arranque de la tabla dinámica se definen fila y columna de inicio. Esto se aprecia en la Figura 52
 |
| Figura 52 Sensibilidad con dos variables |
Al construir la tabla de sensibilidad, debe indicarse entonces tanto la celda fila sensible como la celda-columna sensible, tal como se aprecia en la Figura 53
 |
| Figura 53 Definición de dos variables sensibles |
Los resultados son los presentados en la Figura 54
 |
| Figura 54 Resultados de Tabla sensible de dos variables |
Aunque los valores de entrada, pueden ser cambiados, así como las fórmulas base, no se puede modificar el contenido de las celdas interiores de la tabla. Si se comete algún error, se tendrá que borrar todo el rango de la hoja ocupado por la tabla de sensibilidad
Desarrollar una tabla de sensibilidad, para calcular la tasa periódica de naturaleza vencida equivalente, según lo presentado en la Figura 55
 |
| Figura 55 Modelo Taller Sensibilidad |
La herramienta Escenarios, permite cambiar las variables de una hoja de cálculo en un cuadro de diálogo, manteniendo los valores originales en la misma. Para ello, ésta debe contener celdas de datos susceptibles de ser modificados y celdas de cálculo de contenido invariable cuyas fórmulas utilizan las celdas de datos como parámetros.
Crear un escenario, consiste en definir las celdas de datos variables para habilitar un cuadro de diálogo en el que poder insertar valores nuevos sin modificar la hoja de cálculo.
Para entender este tema, se presenta un ejemplo
Una empresa financiera dedicada al alquiler de vehículos, analiza la posibilidad de comprar y alquilar un bus, el cual tiene un costo de 170.000 €, un plazo de amortización de 8 años y un valor de rescate de 3.000 €.
El contrato de alquiler es por 8 años y se estima una renta anual constante de 27.200 € pospagable
Calcular el valor actual del contrato de alquiler si el tipo de interés anual es de 5.8%
· Desarrollo del ejercicio
Se diseñará una hoja de cálculo que permita calcular el valor actual del contrato, de forma que si se cambia cualquier dato no se deba modificar la fórmula.
Antes de continuar, se explicará la función valor actual VA()
Dicha función, devuelve el valor actual de una inversión. El valor actual es el valor que tiene actualmente la suma de una serie de pagos que se efectuarán en el futuro. Por ejemplo, cuando pide dinero prestado, la cantidad del préstamo es el valor actual para el prestamista.
Sintaxis: VA(tasa;nper;pago;vf;tipo)
o Tasa: Es la tasa de interés por período. Por ejemplo, si obtiene un préstamo para un automóvil con una tasa de interés anual del 10 por ciento y efectúa pagos mensuales, la tasa de interés mensual será del 10%/12 o 0,83%. En la fórmula escribiría 10%/12, 0,83% o 0,0083 como tasa.
o Nper: Es el número total de períodos de pago en una anualidad. Por ejemplo, si obtiene un préstamo a cuatro años para comprar un automóvil y efectúa pagos mensuales, el préstamo tendrá 4*12 (ó 48) períodos. La fórmula tendrá 48 como argumento nper.
o Pago: Es el pago efectuado en cada período, que no puede variar durante la anualidad. Generalmente el argumento pago incluye el capital y el interés, pero no incluye ningún otro arancel o impuesto. Por ejemplo, los pagos mensuales sobre un préstamo de 10.000 $ a cuatro años con una tasa de interés del 12 por ciento para la compra de un automóvil, son de 263,33 $. En la fórmula escribiría -263,33 como el argumento pago. Si se omite el argumento pago, deberá incluirse el argumento vf.
o Vf: Es el valor futuro o un saldo en efectivo que desea lograr después de efectuar el último pago. Si el argumento vf se omite, se asume que el valor es 0 (por ejemplo, el valor futuro de un préstamo es 0). Si desea ahorrar 50.000 $ para pagar un proyecto especial en 18 años, 50.000 $ sería el valor futuro. De esta forma, es posible hacer una estimación conservadora a cierta tasa de interés y determinar la cantidad que deberá ahorrar cada mes. Si se omite el argumento vf, deberá incluirse el argumento pago.
o Tipo: Es el número 0 ó 1 e indica el vencimiento de los pagos
Continuando con el ejercicio, se desarrolla el modelo para calcula el valor actual del contrato, tal como se presenta en la Figura 56
 |
| Figura 56 Modelamiento del Ejemplo de escenarios |
Supongamos ahora que la empresa financiera, antes de firmar el contrato, quiere comparar el valor del contrato para tres casos diferentes, según lo presentado en la Tabla 10
|
|
| Tabla 10 Casos de evaluación – Ejemplo de escenarios |
Los cobros, vencen para los tres casos al final del período.
Así entonces los datos variables son la renta y la periodicidad de la renta.
Para hacer la evaluación, se crean tres escenarios, lo cual se hace mediante el menú herramientas y Escenarios, como se presenta en la Figura 57
 |
| Figura 57 Definición de Escenarios |
Una vez aparece la ventana indicada en la Figura 57, se hace clic sobre agregar, de forma que en este primer paso se definen las celdas variables (Renta y periodicidad (B3- B4) (Figura 58)
 |
| Figura 58 Preparación de escenarios |
El paso siguiente, es el de definir los tres escenarios
 |
| Figura 59 Definición Escenario Semestral |
|
|
| Figura 60 Definición Escenario Trimestral |
 |
| Figura 61 Definición Escenario Mensual |
Una vez se han definido los escenarios, la ventana de definición queda como se indica en la Figura 62
 |
| Figura 62. Escenarios Definidos |
Se hace un clic sobre la pestaña resumen, y se despliega el recuadro adjunto en la Figura 63
|
|
| Figura 63 Recuadro resultados escenarios |
AL hacer clic sobre aceptar, se despliegan los resultados de los tres escenario y el resultado original, esto se presenta en la figura 64
 |
| Figura 64 Resumen de Resultados |
Al analizar los resultados, la opción mas rentables es la de la renta mensual constante, ya que refleja un valor actual de 178.211 €
Para que el lector analice las bondades de estas dos herramientas, se presenta un ejemplo unificando ambos conceptos
o Siguiendo con el caso de la empresa dedica a la renta de vehículos (indicado en el ítem 4.2.1), y sabiendo que el costo del bus es de 170.000 €, y la empresa decide cobrar una renta mensual de 2.300 €, se calculará que tasa de interés de mercado es mas atractiva. Y para ello, se realizará una sensibilidad variando el interés entre 6% y 8,25% con incrementos de 0.25%
o Ahora en la celda A10, introducimos el nombre “Análisis de Sensibilidad”
o En la celda A11, se escribe, “Tasa de Interés”
o En el rango B11:K11, se introducen los valores de las tasas de interés
o La celda A12, recoge el valor del valor actual que esta en E3 (=E3)
o Ahora se selecciona la tabla de sensibilidad con la celda variable FILA (B8), y se tiene el resultado presentado en la Tabla 11
 |
| Tabla 11 Resultado Sensibilidad Ejemplo conjunto con escenarios |
Terminar el ejercicio anterior, realizando una tabla de sensibilidad de dos variables, en función del importe de alquiler mensual y el tipo de interés y con las siguientes variaciones:
Tasas de interés: 6% a 8,25% con incrementos de 0,25%
Renta entre 2200 y 2450 €, con incrementos de 25 €
Ayuda: Celda de Entrada Fila (=B8) / Celda de entrada columna (=B3)
El resultado parcial, se presenta en la Tabla 12
 |
| Tabla 12 Resultados parciales sensibilidad dos variables |
o Pregunta desde que momento la operación deja de ser rentable? (Ayuda compare los valores de la renta con el costo de bus)
La función buscar objetivo resuelve ecuaciones de una variable. Se utilizan para hallar el valor que debe tomar una variable específica, incluida en una fórmula, para igualar esta última a un resultado determinado.
Retomando el ejemplo anterior (ítem 4.2.1), supongamos que la empresa desea calcular el importe por el alquiler del bus que debería cobrar, de forma que, sea cual sea la periodicidad de cobro, esta renta le proporcione un interés del 7% anual.
Con los datos, indicados, el resultado del ejercicio es el que se presenta en la Figura 65
 |
| Figura 65 Datos para aplicar Buscar Objetivo |
Lo que se desea saber es que renta debe tenerse para que el valor actual del contrato sea de -170.000 €. Y para ello recurrimos a Buscar Objetivo, el cual se encuentra en el menú de herramientas – buscar objetivo, tal como se indica en la Figura 66
 |
| Figura 66 Función Buscar Objetivo |
Al hacer clic sobre la opción, aparece el recuadro adjunto (Figura 67)
 |
| Figura 67 Opciones Buscar Objetivo |
Acá, Celda Objetivo, es el resultado que se desea obtener, y que para este caso es el valor actual del contrato (Celda E3)
Con el valor, es el resultado de -170.000 €
Para cambiar la celda: es la celda variable, por tanto el valor de alquiler (B3)

Con estos parámetros, el resultado al dar aceptar es el que se indica en la Figura 68
|
|
| Figura 68 Resultado de la aplicación de Buscar Objetivo |
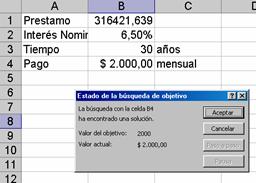
Supongamos que se desea conocer el monto máximo de un préstamo a 30 años que se puede afrontar con una tasa de interés del 6.5% si las cuotas mensuales se limitan a 2000 USD
Para realizar esto, primero debe establecerse la formulación adecuada, para el ejemplo se usa la función Pago,

Para hacer la simulación, el menú herramientas proporciona la herramienta adecuada

Al activar dicha opción, aparece la siguiente ventana

Donde se quiere que la celda que contiene la fórmula B4 (Celda a Definir), de cómo resultado –2000, y para ese pago de 2000USD mensuales que préstamo (B1-Celda a Cambiar) se puede hacer a 30 años

Al dar aceptar, el resultado es:
Otra simulación, sería e determinar cual es el interés a pagar si la cuota es de 2000 ISD mensuales, para un préstamo de 500000 USD a 30 años.
Para ello, solo debe existir formulación referenciada a celdas en la cela objetivo, y por lo tanto la tasa y el tiempo deben indicarse en meses y la tasa mensual (periódica). Adicionalmente dentro de las celdas respectivas de tiempo y tasa, debe estar el valor y no formulas como 6.50%/12 ó 30*12

Así al aplicar la simulación, se tiene:


A efectos de presentar varios ejemplos de Buscar objetivo, se explicarán dos funciones financieras
· Valor Presente Neto
Calcula el valor neto presente de una inversión a partir de una tasa de descuento y una serie de pagos futuros (valores negativos) e ingresos (valores positivos).
Sintaxis: VNA(tasa;valor1;valor2; ...)
Tasa es la tasa de descuento a lo largo de un período.
Valor1, valor2, ... son de 1 a 29 argumentos que representan los pagos e ingresos.
Valor1; valor2; ... deben tener la misma duración y ocurrir al final de cada período.
VNA usa el orden de valor1; valor2; ... para interpretar el orden de los flujos de caja. Asegúrese de introducir los valores de los pagos y de los ingresos en el orden adecuado.
Los argumentos que consisten en números, celdas vacías, valores lógicos o representaciones textuales de números se cuentan; los argumentos que consisten en valores de error o texto que no se puede traducir a números se pasan por alto.
Si un argumento es una matriz o referencia, sólo se considerarán los números en esa matriz o referencia. Se pasan por alto las celdas vacías, valores lógicos, texto o valores de error en la matriz o en la referencia.
Observaciones
La inversión VNA comienza un período antes de la fecha del flujo de caja de valor1 y termina con el último flujo de caja de la lista. El cálculo VNA se basa en flujos de caja futuros. Si el primer flujo de caja ocurre al inicio del primer período, el primer valor se deberá agregar al resultado VNA, que no se incluye en los argumentos valores. Para obtener más información, vea los ejemplos a continuación.
VNA es similar a la función VA (valor actual). La principal diferencia entre VA y VNA es que VA permite que los flujos de caja comiencen al final o al principio del período. A diferencia de los valores variables de flujos de caja en VNA, los flujos de caja en VA deben permanecer constantes durante la inversión. Para obtener más información acerca de anualidades y funciones financieras, vea VA.
VNA también está relacionado con la función TIR (tasa interna de retorno). TIR es la tasa para la cual VNA es igual a cero: VNA(TIR(...), ...) = 0.
Ejemplo 1

Ejemplo 2

Devuelve la tasa interna de retorno de los flujos de caja representados por los números del argumento valores. Estos flujos de caja no tienen por que ser constantes, como es el caso en una anualidad. Sin embargo, los flujos de caja deben ocurrir en intervalos regulares, como meses o años. La tasa interna de retorno equivale a la tasa de interés producida por un proyecto de inversión con pagos (valores negativos) e ingresos (valores positivos) que ocurren en períodos regulares.
Sintaxis: TIR(valores;estimar)
Valores es una matriz o una referencia a celdas que contienen los números para los cuales desea calcular la tasa interna de retorno.
El argumento valores debe contener al menos un valor positivo y uno negativo para calcular la tasa interna de retorno.
TIR interpreta el orden de los flujos de caja siguiendo el orden del argumento valores. Asegúrese de introducir los valores de los pagos e ingresos en el orden correcto.
Si un argumento matricial o de referencia contiene texto, valores lógicos o celdas vacías, esos valores se pasan por alto.
Estimar es un número que el usuario estima que se aproximará al resultado de TIR.
Microsoft Excel utiliza una técnica iterativa para el cálculo de TIR. Comenzando con el argumento estimar, TIR reitera el cálculo hasta que el resultado obtenido tenga una exactitud de 0,00001%. Si TIR no llega a un resultado después de 20 intentos, devuelve el valor de error #¡NUM!
En la mayoría de los casos no necesita proporcionar el argumento estimar para el cálculo de TIR. Si se omite el argumento estimar, se supondrá que es 0,1 (10%).
Si TIR devuelve el valor de error #¡NUM!, o si el valor no se aproxima a su estimación, realice un nuevo intento con un valor diferente de estimar.
Observaciones
TIR está íntimamente relacionado a VNA, la función valor neto actual. La tasa de retorno calculada por TIR es la tasa de interés correspondiente a un valor neto actual 0 (cero). La fórmula siguiente demuestra la relación entre VNA y TIR:
VNA(TIR(B1:B6),B1:B6) es igual a 3,60E-08 [Dentro de la exactitud del cálculo TIR, el valor 3,60E-08 es en efecto 0 (cero).]
Ejemplo

Taller 1
| Suponga que tiene una serie de resultados previstos en
caja al final de 10 periodos con un valor presente negativo y una Tir
negativa. Le piden determine usted que flujo debe haber en determinado
periodo para que el VPN pase a ser cero
Los valores son
|
 |
Taller 2
| Un almacén vende un juego de alcoba con valor de contado
de 1.500.000 y a plazos tiene los siguientes planes:
a- Cuota inicial 600.000 y dos cuotas 3 y 6 meses después con valores de 400.000 y 584.362 respectivamente b- Tres cuotas de 400.000 que deben entregarse hoy (cuota inicial) a los 4 y 8 meses y una cuota última al mes 12 de 493.429,36 Cual plan presenta la menor financiación (TIR), y que valor presente neto da cada plan con cada TIR?
|
Taller 3
| Si Compro una máquina por 900.000 USD, vida útil de 3 años y un valor de salvamento de 100.000 USD., Debo repararla dos años después de comprada a un costo de 80.000 USD. Si la máquina produce ingresos de 400.000 USD al final de cada año. Debo comprarla? Tasa efectiva 24% |
 |
Taller 4
| Al comprar una moto quede debiendo 1.000.000 y tengo 2
opciones de pago:
a- A los 4 meses 500.000 y a los 7, 667.119,46 b- Pagar a los 7 meses 1.246.688,59 Que opción es mejor, tasa: 2.5% mes
|
 |
Taller 5
| Se necesita comprar una máquina. En el mercado se
encuentran de tipo A y B con iguales rendimientos industriales y precio de
contado 1.080.000 y 1.100.000 respectivamente. A crédito, se adquieren
así:
Máquina A: cuota inicial 500.000 y dos cuotas en los 3 y 6 meses de 400.000 y 261.016,24 respectivamente Maquina B: Cuota inicial 700.000 y una cuota a los 6 meses por 487027,67. A que interés es indiferente utilizar cualquiera de los dos máquinas
|
 |
Usando “Buscar Objetivo”, elaborar una tabla de amortización para analizar el comportamiento de una suma de $3.000.000 en 12 pagos periódicos uniformes con una tasa del 3% para los 3 primeros períodos, 3.5% para los siguientes 3, 4% para los siguientes 3 y 2% para los 3 últimos períodos. Respuesta: Cuota: 306.147
Con la estructura del ejemplo anterior, elaborar una tabla de amortización suponiendo que las cuotas crecen un 10% cada período. Respuesta: Cuota Período 1: 178.183,97
Usando la misma estructura básica, elaborar la tabla con pagos creciendo en forma escalonada, cada 4 pagos se incrementa la cuota un 20% (Escalonamiento Geométrico): Respuesta: Cuota Período 1: 256.400
Usando la misma estructura básica, elaborar la tabla con pagos decrecientes en $40.000 por bloques de tres pagos (Gradiente escalonado decreciente): Respuesta: Cuota Período 1: 361.266
Elaborar una tabla de amortización, para analizar el comportamiento de $1.000.000 en pagos mensuales uniformes con un plazo de 18 meses, la financiera cobra una tasa durante los primeros 8 meses de 2.5% periódico mensual, de ahí en adelante cada mes la tasa sube 0.3 puntos. El deudor solicita que el periodo 1 y el 8 sean de gracia, y además ofrece un pago extra de 100.000 en el periodo 12: Respuesta: Cuota Período 2: 76.394
Elaborar una tabla para capitalizar la suma de $15.000.000 en 12 pagos trimestrales crecientes de $100.000 con una cuota extra de $300.000 en el periodo 4, la tasa trimestral es del 7%: Respuesta: Cuota 1: 339.463
Cual puede ser el préstamo máximo que se le puede conceder a una persona que dice puede pagar mensualmente $60.000 durante 15 meses y que en el mes 12 además de la cuota de 60.000 puede pagar una cuota extraordinaria de 250.000, Suponga una tasa del 3.5% mensual: Respuesta: Préstamo. 856.490
Una deuda de 4.000.000 con interés del 3.2% mensual, se va a cancelar mediante 12 pagos mensuales de $250.000 y una cuota extra adicional en el período 8. Cuanto es la cuota extra? Respuesta: 1.982.557
Una deuda de 3.000.000 se cancela en 12 pagos mensuales de $306.809. Cual es la tasa periódica mensual que amortiza la deuda?: Respuesta: 3.3%
Cuando se trató de la función buscar objetivo (ítem 4.4), se entendió que dicha herramienta solucionaba 1 ecuación con una incógnita. Pero en cualquier situación financiera, es muy factible encontrar muchas variables, condiciones o aspectos fijos que conducen a una solución de muchas ecuaciones y una sola incógnita.
Solver es una herramienta de Excel, que resuelve problemas de programación lineal. Un programa lineal es un sistema que optimiza (Maximiza o minimiza) el resultado de una ecuación, teniendo en cuenta una serie de restricciones fijadas sobre sus variables y que se traduce en ecuaciones o inecuaciones. Y esto es precisamente el problema que se indicó en el párrafo anterior
Cuando el Excel, se instala por primera vez en un equipo, quedan funciones sin activar debido a que el común de los usuarios no las utilizan, pero su inactivación no indica que al momento de requerirse sea necesario reinstalar el software.
Una de estas funciones es el Solver, el cual se activa de la siguiente manera:
El menú de herramientas, se encuentra la opción complementos, con la cual se le indica a Excel que hay una funciones que deben ser activadas siempre que se use Excel, tal como se indica en la Figura 69
 |
| Figura 69 Activación de funciones en Excel |
Como se aprecia en la Figura 69, debe hacerse un chequeo sobre el recuadro de Solver, adicionalmente, se recomienda haga un chequeo a dos opciones mas: Herramientas para análisis y herramientas para análisis – VBA, debido a que al activas estas dos opciones Excel dispone de mas funciones para el usuario, varias de ellas útiles para cálculos financieros
Como se indicó al inicio de esta sección, el solver, es una herramienta para solucionar problemas de programación lineal. Este sistema requiere de unas estimaciones matemáticas. Aunque Solver trae la opción para cambiar dichos parámetros, estos es necesario cambiarlos a la instalación original del programa. Dichos cambios son necesarios cuando se analizan problemas de ingeniería de mayor precisión, mas no para problemas de aspectos financieros.
Pero a nivel informativo, se presentan en este aparte, las opciones de configuración matemática de dicha herramienta.
Desde Herramientas – Solver (botón Opciones...) tenemos varias opciones para configurar Solver (Figura 70).
 |
| Figura 70 Menu de configuración matemática de Solver |
Pueden controlarse las características avanzadas del proceso de solución, cargarse o guardarse definiciones de problemas y definirse parámetros para los problemas lineales y no lineales. Cada opción tiene una configuración predeterminada adecuada a la mayoría de los problemas.
La descripción de las opciones es:
Tiempo máximo: Limita el tiempo que tarda el proceso de solución. Puede introducirse un valor de hasta 32.367, pero el valor predeterminado 100 (segundos) es adecuado para la mayor parte de los problemas.
Iteraciones: Limita el tiempo que tarda el proceso de solución, limitando el número de cálculos provisionales. Aunque puede introducirse un valor de hasta 32 767, el valor predeterminado 100 es adecuado para la mayor parte de los problemas pequeños.
Precisión: Controla la precisión de las soluciones utilizando el número que se introduce para averiguar si el valor de una restricción cumple un objetivo o satisface un límite inferior o superior. Debe indicarse la precisión mediante una fracción entre 0 (cero) y 1. Cuantos más decimales tenga el número que se introduzca, mayor será la precisión; por ejemplo, 0,0001 indica una precisión mayor que 0,01. Cuanto mayor sea la precisión, más tiempo se tardará en encontrar una solución.
Tolerancia: El porcentaje mediante el cual la celda objetivo de una solución satisface las restricciones externas puede diferir del valor óptimo verdadero y todavía considerarse aceptable. Esta opción sólo se aplica a los problemas que tengan restricciones enteras. Una tolerancia mayor tiende a acelerar el proceso de solución.
Convergencia: Si el valor del cambio relativo en la celda objetivo es menor que el número introducido en el cuadro Convergencia para las últimas cinco iteraciones, Solver se detendrá. La convergencia se aplica únicamente a los problemas no lineales y debe indicarse mediante una fracción entre 0 (cero) y 1. Cuantos más decimales tenga el número que se introduzca, menor será la convergencia; por ejemplo, 0,0001 indica un cambio relativo menor que 0,01. Cuanto menor sea el valor de convergencia, más tiempo se tardará en encontrar una solución.
Adoptar modelo lineal: Selecciónelo cuando todas las relaciones en el modelo sean lineales y desee resolver un problema de optimización o una aproximación lineal a un problema no lineal.
Mostrar resultado de iteraciones: Selecciónelo para que Solver muestre temporalmente los resultados de cada iteración. Esta opción es válida sólo en modelos no lineales.
Usar escala automática: Selecciónelo para utilizar la escala automática cuando haya grandes diferencias de magnitud entre las entradas y los resultados; por ejemplo, cuando se maximiza el porcentaje de beneficios basándose en una inversión de medio millón de dólares.
Adoptar no-negativo: Hace que Solver suponga un límite de 0 (cero) para todas las celdas ajustables en las que no se haya definido un límite inferior en el cuadro Restricción del cuadro de diálogo Agregar restricción.
Cargar modelo: Muestra el cuadro de diálogo Cargar modelo, donde puede especificarse la referencia del modelo que desee cargar.
Guardar modelo: Muestra el cuadro de diálogo Guardar modelo, donde puede especificar la ubicación en que desee guardar el modelo. Úselo únicamente cuando desee guardar más de un modelo con una hoja de cálculo; el primer modelo se guardará de forma automática.
Estimación: Especifica el enfoque que se utiliza para obtener las estimaciones iniciales de las variables básicas en cada una de las búsquedas dimensionales.
· Lineal: Utiliza la extrapolación lineal de un vector tangente.
· Cuadrática: Utiliza la extrapolación cuadrática, que puede mejorar en gran medida los resultados de problemas no lineales.
Derivadas: Especifica la diferencia que se utiliza para estimar las derivadas parciales del objetivo y las funciones de la restricción.
· Progresivas: Se utilizan para la mayor parte de los problemas, en que los valores de restricción cambien relativamente poco.
· Centrales: Se utiliza en los problemas en que las restricciones cambian rápidamente, especialmente cerca de los límites. Aunque esta opción necesita más cálculos, puede ser útil cuando Solver devuelve un mensaje diciendo que no puede mejorarse la solución.
Buscar. Especifica el algoritmo que se utiliza en cada iteración para determinar la dirección en que se hace la búsqueda.
· Newton: Utiliza un método cuasi Newton que normalmente necesita más memoria pero menos iteraciones que el método de gradiente conjugado.
· Gradiente Conjugado: Necesita menos memoria que el método Newton, pero normalmente necesita más iteraciones para alcanzar un determinado nivel de precisión. Use esta opción cuando se trate de un problema grande o cuando al hacer un recorrido a través de iteraciones se descubra un progreso lento.
Se planea la campaña de publicidad de un nuevo producto con las siguientes condiciones:
Presupuesto total: 12’000,000
Mensajes que deben llegar a los consumidores mediante publicidad escrita en diferentes medios: mínimo 800 millones
Publicaciones o medios escritos disponibles: 6
Los costos de cada publicación son diferentes (Pub1, Pub2, Pub3, Pub4, Pub5, Pub6)
Cada publicación exige mínimo 6 anuncios
En una sola publicación no se debe gastar mas de 1/3 del presupuesto total
Los costos agrupados de las publicaciones tipo 3 y 4 no debe exceder 7’500.000
Lo primero que debe hacerse es crear el archivo Excel, con el que se podrán estimar los costos, según lo indicado en la Figura 71
 |
| Figura 71 Modelo de Datos Campaña de Publicidad |
En la Figura 71, se aprecian para cada publicación, los costos por aviso, la audiencia que garantizan con cada aviso y los anuncios mínimos a contratar
Se aprecia igualmente, la zona de restricciones:
Presupuesto total
Presupuesto restringido para las Publicaciones 2 y 3
Audiencia mínima exigida
Participación máxima de cada publicación en el presupuesto total
Anuncios mínimos a contratar por publicación.
Y es claro que lo que se busca es calcular el mínimo presupuesto posible, pero que sea mayor a 12’000.000 que se logre con la combinación de los 6 medios disponibles y cumpliendo las restricciones.
Esto es algo que con Buscar Objetivo es imposible
Al implementarse el solver, se deben cubrir varias etapas:
Definición del Objetivo
Aplicación de restricciones
Buscar la solución
Para realizar todo esto debemos buscar entonces en el menú de herramientas el Solver, esto se aprecia con la Figura 72
 |
| Figura 72 Implementación del Solver |
En esta etapa se puede hacer un símil con la función Buscar Objetivo, y es en esencia determinar la celda del resultado que debemos obtener y que es la que me resumen el presupuesto total calculado (celda objetivo)
El objetivo es conseguir el valor minino a 12’000.000, y que se logra cambiando la contratación de anuncios por publicación (Celdas cambiantes)
Presupuesto <=12’000.000
Presupuesto Publicación 3 + Publicación 4 <=7’500.000
Audiencia >= 800 Millones de Personas
Anuncios por publicación >=6
% de cada publicación sobre el presupuesto total <=33.33%
Los anuncios deben ser números enteros (no es posible contratar medio 1,1 anuncios)
La implementación de los valores, se presenta en la Figura 73
 |
| Figura 73 Implementación del Solver de Publicidad |
La definición de la celda objetivo y de las celdas cambiantes se hace simplemente indicando con el Mouse las celdas respectivas
Para la definición de restricciones hay una consideración adicional:
Estas ecuaciones, se incluyen en la zona denominada “sujetas a las siguientes restricciones..” (Figura 73), para lo cual debe hacerse un clic sobre agregar y entonces aparece la ventana o recuadro presentado en la Figura 74
 |
| Figura 74 Recuadro para incluir restricciones |
La forma de crear las restricciones es la misma, independiente de la restricción que se tenga. Vamos a hacer la de Presupuesto 3 + Presupuesto 4 <=7’500.000
De la Figura 73, se puede apreciar que la celda que me resumen ambos costos es la E11, y que esta celda debe ser menor o igual a la restricción de 7’500.000 (celda e21). Para determinar los signos simplemente se abre el combo de selección de signos, tal como se indica en la Figura 75
 |
| Figura 75 Creación de una restricción |
Aplicando el mismo procedimiento para todas las restricciones, se llega lo que se presenta en la Figura 76
 |
| Figura 76 Definición total de restricciones |
Una vez implementado el solver, se hace clic sobre resolver, y aparece lo siguiente:
 |
| Figura 77 Solución del Solver |
AL dar aceptar con el Mouse, se puede apreciar la respuesta, que en efecto cumplió con el objetivo (11’186.170 – mínimo valor), cumpliendo con todas las restricciones
La opción de informes, es simplemente la memoria de cálculo del Excel al problema propuesto, y los cuales deben ser marcados con el Mouse, al momento de Excel indicar que encontró una respuesta

Estos reportes quedan en una hoja adicional del libro de Excel y contiene la información indicada en la Figura 78
 |
| Figura 78 Memoria de cálculo de la solución |
Si se detecta que existió un error en la implementación del solver (Celda objetivo o celdas cambiantes o restricciones), esto se puede modificar simplemente con entrara a la opción solver nuevamente. Este procedimiento es muy flexible
En una tienda de electrodomésticos, se quiere lanzar un oferta de neveras a $500.000 y secadoras a $450.000, La venta de cada nevera toma 10 minutos al vendedor y 5 minutos al instalador. La secadora requiere de 8 minutos al vendedor y 12 minutos al instalador. Se dispone de 4 vendedores y 3 instaladores, que trabajan 4 horas diarias
Cuantas neveras y cuantas secadoras interesa poner a la venta durante 20 días que dura la campaña?
La solución empieza con la construcción del modelo de datos (Figura 79)
 |
| Figura 79 Modelo de datos ejemplo electrodomésticos |
El problema consiste en determinar el número de neveras y secadoras a vender durante 20 días de forma que se maximicen los ingresos por la venta, por lo tanto calcule en E5 lo que sería la venta de neveras y secadoras, que es:
![]()
Como el tiempo de vendedores e instaladores es limitado, debe calcularse el tiempo total de minutos por personal (vendedor e instalador) durante 20 días, esto lo debe formular en las celdas e16 y E17 y que es básicamente:
![]()
![]()
Luego debe calcularse el tiempo invertido por el personal total según el número de neveras y secadoras vendidas, y que básicamente es:
![]()
![]()
Ahora debe implementarse la solución en SOLVER
Celda Objetivo: Ingresos maximizados (E5)
Valor de la celda objetivo : Máximo
Celda a cambiar: Total de Neveras y secadoras (D2 y D3)
Restricciones:
Total requerido por vendedores debe ser menor o igual a o calculado para 20 dias, así mismo para los instaladores
A efectos de que Solver calcule mas rápidamente, los valores de cantidad de neveras y secadores deben ser números enteros y mayores que cero,
 |
| Figura 80 Recuadro Restricciones Solver electrodomésticos |
Una vez implementado, se llega a la solución indicada en la Figura 81
 |
| Figura 81 Solver Electrodomésticos - Solución Final |
Una empresa europea fabrica remaches, el precio un unitario de venta es 1,25 Euros, su nivel de producción diario es de 100 unidades, los cuales vende sin dejar remanente.
Los costos fijos de la empresa son 5 Euros y los costos variables por unidad construida son de 1 euro. Con dichos valores el beneficio es 20 euros.
Se desea aumentar el beneficio a 40 euros sin variar el precio de venta. Y con los siguientes limites: Costos Fijos Min 3, max 5. Y costos variables Min 0.8, max 1
Objeto:
· Beneficio =(100*Precio de Venta)-(100 * Costo Unitario + Costo Fijo)=40
· Variando: Costo Fijo y Costo Variable
· Restricciones:
· Costo Fijo: Mínimo 3 – Máximo 5
· Costo Variable: Mínimo 0,1 – Máximo 0,8
Luego de implementar solver, se llega a la solución presentada en la Figura 82
 |
| Figura 82 Solver Remaches |




Respuesta

Usted ha ganado 100.000 USD y decide invertir en un portafolio de acciones cuyo nombre, denominación y rentabilidad anual, se presentan a continuación:
· CAE Inc:
o Sigla CGT
o Precio hoy de la acción: 60 USD
o Rendimiento anual de la acción: 7 USD
· ABB Ltda:
o Sigla ABB
o Precio hoy de la acción: 25 USD
o Rendimiento anual de la acción: 3 USD
· Seven Eleven:
o Sigla SE
o Precio hoy de la acción: 20 USD
o Rendimiento anual de la acción: 3 USD
Se tienen las siguientes restricciones de máxima inversión:
· CAE: 60.000 USD
· ABB: 25.000 USD
· Seven Eleven: 30.000 USD
Determine el número de acciones por tipo de acción a efectos de maximizar el rendimiento del portafolio
Una cadena de montaje de vehículos es capaz de ensamblar hasta 80.000 vehículos al mes, de dos tipos (A-B). Los gastos de producción de cada vehículo no deben sobrepasar los siguientes topes:
Tipo A: 900.000 Pesetas
Tipo B: 660.000 Pesetas
Los gastos totales de producción al mes no han de superar los 60.000 millones de pesetas.
Las utilidades por tipo de vehículo son:
Tipo A: 210.000Pesetas
Tipo B: 150.000 Pesetas
Cuantos vehículos por cada tipo se deben fabricar para obtener una ganancia máxima?. Si se tienen dos casos:
Deben producirse por lo menos 10.000 unidades de cada tipo.
Deben producirse al menos 1 unidad por tipo
Una urbanización construirá 2 tipos de casas (A-B). La empresa constructora dispone de 300 millones de pesetas, siendo el costo de cada casa de 6.4 y 4 millones respectivamente. Además las casas del tipo A, han de ser el 40% por lo menos del total, y las de tipo B por lo menos el 20%.
Si el Beneficio es de 1,5 millones de pesetas por el tipo A , y 1 millón por el tipo B.
Cuantas casas deben construirse de cada tipo y así obtener un beneficio máximo. Teniendo presente que debe construirse al menos una cada por tipo
Una sociedad que quiere producir herramientas de metal, requiere hacer una previsión a 5 años de lo que puede ser el negocio, y ver el beneficio o pérdida al final del quinto año.
Cuenta con los siguientes datos:
Ventas esperadas el primer año, 100.000 unidades
Precio estimado de venda por unidad: 800 Pesetas
Incremento de venta esperado: 8% anual, con respecto al año anterior
Gastos fijos estimados: 1’000.000 el primer año, y se cree incrementen 5% cada año con respecto al anterior
No se sabe cuanto debe ser el personal a contraer, pero se han hecho pruebas y se ha visto que se tarda 10 minutos producir una unidad, cada empleado trabaja 1800 horas año y los gastos salariales son de 3’500.000 pesetas por empleado
Finalmente, se sabe que se gastan 100 gr de materia prima por cada unidad producida. El costo básico de materia prima es de 5.000 Pesetas/kg. Pero se puede conseguir un descuento dependiendo de la cantidad comprada, así:
· De 10.000kg a menos de 12.000, 5% de descuento
· De 12.000kg a menos de 14.000, 7% de descuento
· De 14.000kg a menos de 15.000, 8% de descuento
· De 15.000 kg en adelante, 9% de descuento
Se ha adquirido maquinaria por 2’000.000 de pesetas mediante un leasing a 5 años y un valor de recompra del 10% a un interés del 55%
Se requiere hacer una previsión a 5 años para ver el resultado de la empresa a 5 años, teniendo presente los impuesto del 35%
Se obtiene beneficio al año 5?
Cual es el precio de venta para obtener un beneficio acumulado de 5’000.000 de pesetas al final del quinto año?
Los estudios de mercadeo, no dan datos precisos para el primer año, de modo que sería conveniente hacer un estudio y ver que pasa si se sensibilizan las ventas entre 80.000 y 120.000 unidades