|
|
|
 Análisis
de regresión múltiple
Véalo
aquí
Para dos variables independientes, la fórmula general de la
ecuación de regresión múltiple es:
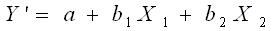
X1 y X2 son las variables independientes.
a es la intercepción en Y.
b1 es el cambio neto en Y por cada cambio unitario en X1,
manteniendo X2 constante. Se denomina coeficiente de regresión
parcial, coeficiente de regresión neta o bien coeficiente de
regresión.
La ecuación general de regresión múltiple con k varibles
independientes es:
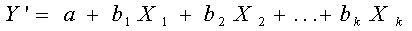
El criterio de mínimos cuadrados se usa para el desarrollo de esta
ecuación.
Como estimar b1, b2, etc. es muy tedioso, existen muchos programas
de cómputo que pueden utilizarse para estimarlos.
Error estándar múltiple de la estimación
Véalo
aquí
El error estándar múltiple de la estimación es la medida de la
eficiencia de la ecuación de regresión.
Está medida en las mismas unidades que la variable dependiente.
Es difícil determinar cuál es un valor grande y cuál es uno
pequeño para el error estándar.
La fórmula es:
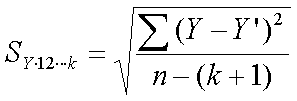
donde n es el número de observaciones y k es el número de
variables independientes.
Regresión y correlación múltiples (suposiciones)
Véalo
aquí
Las variables independientes y dependientes tienen una
relación lineal.
La variable dependiente debe ser continua y al menos con escala de
intervalo.
La variación en (Y - Y’) o residuo debe ser la misma para todos
los valores de Y. Cuando éste es el caso, se dice que la
diferencia presenta homosedasticidad.
Los residuos deben tener distribución normal con media igual a 0.
Las observaciones sucesivas de la variable dependiente no deben
estar correlacionadas.
Tabla
ANOVA
Véalo
aquí
La tabla ANOVA proporciona la variación de la variable
dependiente (tanto de la que está explicada por la ecuación de
regresión como de la que no lo está).
Matriz
de correlación
Véalo
aquí
La matriz de correlación se usa para mostrar todos los
posibles coeficientes de correlación simple entre todas las
variables.
La matriz también se útil para localizar la correlación de las
variables independientes.
En la matriz se muestra qué tan fuerte está correlacionada la
variable independiente con la variable dependiente.
Prueba
global
Véalo
aquí
La prueba global se usa para investigar si todas las variables
independientes tienen coeficientes significativos. Las hipótesis
son:
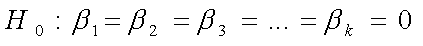
Ha : al menos uno de los coeficientes de regresión no es cero.
El estadístico de prueba es la distribución F con k (número de
variables independientes) y n - (k + 1) grados de libertad, donde
n es el tamaño de la muestra.
Prueba
para variables individuales
Véalo
aquí
La prueba se usa para determinar qué variable independiente
tiene coeficientes de regresión diferentes de 0.
Las variables que tiene coeficientes de regresión cero, suelen
desaparecer del análisis.
El estadístico de prueba es la distribución t con n - (k + 1)
grados de libertad.
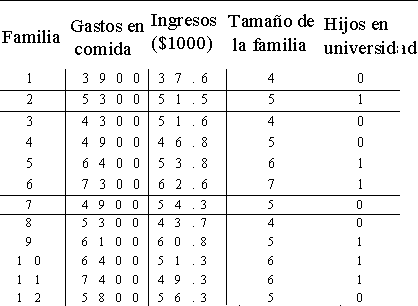
Un estudio de mercado para la cadena de tiendas autoservicio Super
Dollar analiza la cantidad anual que gastan en comida las familias
de cuatro o más miembros. Se iensa que tres variables
independientes se relacionan con los gastos en comida. Esas
variables son: ingreso familiar total, tamaño de la familia y si
la familia tiene hijos en la universidad.
Use un software, como MINITAB o Excel, para desarrollar la
matriz de correlación.
Del análisis proporcionado por MINITAB, escriba la ecuación de
regresión:
¿Qué gastos en comida estima para una familia de 4 integrantes,
sin hijos en la universidad y con ingresos de $50,000?
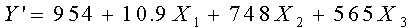Y’=954 + 10.9(50) + 748(4) + 565 (0) = 4491.
Realice una prueba global de hipótesis para determinar si alguno
de los coeficientes de regresión es distinto de cero.
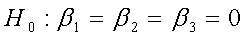H1 : al menos una
H0 se rechaza si F > 4.07
A partir de la salida de MINITAB, el valor del estadístico de
prueba calculado es 10.94
Decisión: como F = 10.94 > 4.07, H0 se rechaza. Entonces, no todos
los coeficientes de regresión son cero.
Realice una prueba individual para determinar qué coeficientes
son distintos de cero.
De la salida de MINITAB, la única variable significativa es FSIZE
(tamaño de familia) al usar los valores p. Las otras variables
pueden omitir del modelo.
Entonces,
Para 5% de nivel de significancia, se rechaza H0 si el valor p <
.05
Como el valor p =.039 <.05, se rechaza H0 y se concluye que .
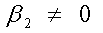Esto es, el tamaño de la familia y cantidad gastada en comida
tienen una relación significativa.
Variables
cualitativas y regresiones escalonadas
Véalo
aquí
Las variables cualitativas son no numéricas y también se
llaman variables ficticias .
Para una variable cualitativa, sólo existen dos condiciones
posibles.
La regresión escalonada conduce a la ecuación de regresión más
eficiente.
Sólo las variables independientes con coeficientes de regresión
significativos entran en el análisis. Las variables se introducen
en el orden en que hacen que R^2 aumente más rápido.
Análisis
de residuos
Véalo
aquí
Un residuo (o residual) es la diferencia entre el valor real
de Y y el valor pronosticado Y’.
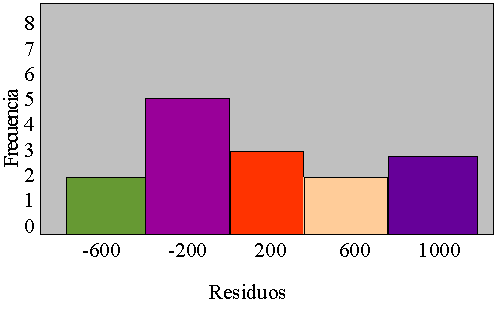
Los residuos deben tener una distribución normal aproximada. Los
histogramas y los diagramas de tallo y hoja sirven para verificar
estos requisitos.
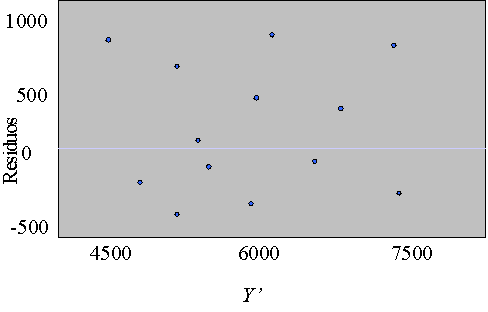
Una gráfica de residuos y los valores de Y’ correspondientes se
usan para mostrar que no hay tendencias ni patrones en los
residuos.
|
|
