Dinámica de sistemas: sus enunciados básicos
System Dynamics: fast guide
Marcelo Claudio Perissé
Universidad Nacional de La Matanza
Resumen - Abstract
Un tutorial básico para modelar, analizar y simular la complejidad de los sistemas empresariales.
A basic tutorial for modeling, analysis and simulate the complexity of business systems.
Palabras Clave - Keyword
Organización y dirección de empresas, Investigación Operativa, Dinámica de Sistemas
Organization and management of enterprises, Operations research, System Dynamics
Un sistema viene representado por una lista de variables.
William Ross Ashby
Contenido
La dinámica de sistemas: una metodología sistémica
Aplicaciones de la dinámica de sistemas
Estructura y comportamiento elemental en dinámica de sistemas
Un lenguaje elemental para la descripción de sistemas: diagramas de influencias
Bucle de realimentación negativa
Bucle de realimentación positiva
Sistemas complejos y estructuras genéricas
De la estructura al comportamiento: diagramas de Forrester
Introducción
En este trabajo abordaremos una perspectiva «sistémica», y por lo cual se espera especificar claramente:
- al conjunto de las partes que lo conforman, y
- a la estructura constituida por las relaciones entre las partes del sistema y que se articulan para constituir una unidad.
La descripción más elemental que podemos hacer de un sistema será:
- enunciando al conjunto de sus partes, y
- estableciendo un esbozo de cómo se influyen entre sí.
Cada uno de estos elementos se pueden ver representados, en la Ilustración 1 por nodos y aristas respectivamente.
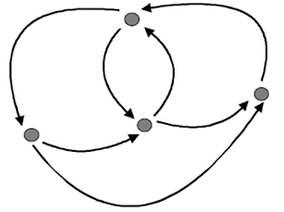
|
|
Más particularmente en la Ilustración 2, se expresa una estructura determinada, en la que el grafo aporta una descripción sobre la naturaleza estructural del sistema. |
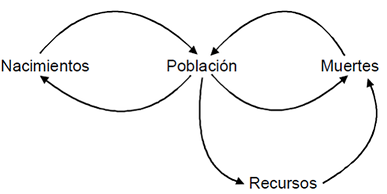 |
Con el término «dinámica» (por oposición al de estática), se expresa el carácter cambiante de aquello que es adjetivado; y se lo puede asociar a una imagen como la que se muestra en la Ilustración 3, que representa la trayectoria de una magnitud.
 |
Cuando las distintas variables de un sistema, que podemos asociar a sus partes, sufren cambios en sus estados a lo largo del tiempo, como consecuencia de las interacciones que se producen entre ellas, nos estamos refiriendo a la «dinámica de sistemas», y entre los principales conceptos útiles en la dinámica de sistemas, veremos:
- Modelo: es un objeto que representa a otro (el modelo al sistema [isomorfismo/homomorfismo]).
- Experimento: proceso de extraer datos de un sistema mediante la activación de sus entradas.
- Simulación: proceso de diseñar un modelo de un sistema, y experimentar con él, para comprender su comportamiento o evaluar nuevas estrategias dentro de específicos criterios- .
El interés de la «dinámica de sistemas» está puesto en el subconjunto de simulaciones matemáticas como descripción codificada de un experimento que hace referencia al modelo al cual se aplica, y que son codificables como programas informáticos.
La dinámica de sistemas: una metodología sistémica
Toda metodología sistémica, se constituye como un instrumento que permite estudiar los problemas resultantes de las interacciones que se producen en el seno de un sistema.
El especialista en sistemas hace uso de una metodología sistémica cuando:
- especifica cuáles son los distintos elementos que conforman un cierto aspecto de la realidad, y
- analiza cómo se produce la integración (cohesión, adhesión) de esos elementos en la unidad del problema que está analizando.
Por lo tanto, tienen tanta importancia las partes que componen al sistema, como éste en su totalidad; en otras palabras:
al considerarse al sistema como una unidad, se hará sin perder de vista las partes que lo conforman; y al considerarse las partes, se hará a sabiendas que son componentes de un todo. Por lo cual, la sistematización aporta una metodología en la que se articula, como un proceso de imbricamiento, el análisis y la síntesis.
Entonces:
- si un sistema es un conjunto de elementos en interacción, y
- si esta interacción es el resultado de que unas partes influyen sobre otras produciendo cambios en los estados de dichas partes (variaión concomitante), por lo tanto
- los cambios que se producen en el sistema son un reflejo de las interacciones existentes.
En este marco, la dinámica de sistemas, mediante el análisis de las relaciones existentes entre los componentes que forman un sistema, permite explicar el comportamiento de dicho sistema como manifestación de sus cambios. En otras palabas:
la «dinámica de sistemas» pone de manifiesto cómo está relacionada la estructura con el comportamiento del sistema.
Así como la metodología sistémica suministra un lenguaje formal que aporta nuevas formas de ver los problemas complejos, queremos destacar que:
las herramientas que aporta la «dinámica de sistemas», como son los diagramas de influencia o los diagramas de flujos, permiten observar, diseñar, y analizar a los sistemas, que están en nuestro entorno, mediante una óptica que facilita el descubrir aquellos aspectos estructurales y funcionales que son relevantes al momento de elaborar políticas, tomar decisiones, y construir sistemas de control, que nos permitan operar sobre la realidad de la empresa o la industria objeto de estudio.
Aplicaciones de la dinámica de sistemas
Javier Aracil (Aracil, 1995) destaca que la dinámica de sistemas es una metodología ideada para resolver problemas concretos. Inicialmente se concibió, bajo el nombre de dinámica industrial, para estudiar en las empresas, aquellos problemas que se presentaban retrasos en la transmisión de información, que unidos a la existencia de estructuras de realimentación, dan lugar a modos de comportamiento de tipo oscilatorio no deseables.
Estructura y comportamiento elemental en dinámica de sistemas
Diagramas de influencias: un lenguaje para la descripción de sistemas
Recordemos que la descripción mínima de un sistema viene dada por:
- la especificación de las distintas partes que lo conforman, y
- las relaciones que se establecen por las influencias de dichas partes.
En la Figura 4, se puede ver un ejemplo de cómo se puede analizar la estructura sistémica de un proceso, que representa el hecho de llenar un vaso con agua.
 |
Su descripción coloquial sería:
Se cuenta con un vaso que tiene una indicación de nivel superior, y una canilla con la que se regula un flujo de agua; y se espera completar el vaso con agua hasta alcanzar el nivel superior. En una descripción procedimental podríamos describirlo así
- se abre la canilla,
- se agrega agua en el vaso,
- se observa el nivel alcanzado en el vaso,
- se compara el nivel alcanzado en el vaso con el nivel deseado:
- si existe alguna diferencia entre el nivel alcanzado y el nivel deseado,
- la canilla se va cerrando según disminuya la diferencia entre el nivel alcanzado y el nivel deseado,
- si no existe diferencias entre el nivel alcanzado y el nivel deseado,
- la canilla se cierra.
En el diagrama se muestran los elementos básicos del proceso y su unión mediante flechas que indican las influencias que se establecen entre ellos. Por ejemplo, el nivel alcanzado depende del flujo de agua o, lo que es lo mismo, el flujo de agua influye sobre el nivel alcanzado, lo que se indica, en el diagrama, mediante una flecha que va desde 'Flujo de agua' a 'Nivel'. Esta relación de influencia se escribe:
Flujo de agua → Nivel
De forma análoga, la 'discrepancia' se determina a partir del 'nivel deseado' y del 'Nivel' alcanzado. Por último, la 'discrepancia' determina el 'flujo de agua'.
Este ejemplo constituye una muestra de cómo, mediante un bosquejo, se puede analizar un sistema, a través de:
- descomponerlo en sus elementos esenciales,
- relacionar estos elementos, y de
- especificar cómo se producen las influencias entre ellos.
La influencia, en esta descripción, se mantiene a un nivel cualitativo, en el sentido de que únicamente se dice si se produce o no una influencia, pero no la forma o magnitud que tiene.
En general, aunque no conozcamos la forma matemática exacta de la función, si 'A' y 'B' son dos partes de un sistema, el hecho de que 'A' influya sobre 'B' se puede representar mediante una flecha de la forma:
A → B, e indica que B es una función de A, es decir
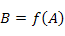
El conjunto de las relaciones entre los elementos de un sistema recibe la denominación de estructura del sistema y se representa mediante el «diagrama de influencias» o causal.
En su forma más simple el diagrama de influencias (ver ilustración 5) está formado por lo que se conoce como un grafo orientado. Las flechas que representan las aristas tendrán asociadas un signo (+; -); este signo indica si las variaciones del antecedente y del consecuente son: del mismo signo (+), o de signo contrario (-).
Será del mismo signo (+), cuando entre A y B exista una relación de influencia positiva, y se representa:
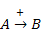
Esto quiere decir que: si A se incrementa, lo mismo sucederá con B; y, por el contrario, si A disminuye, así mismo lo hará B.
Por otra parte, será de signo contrario (-), cuando la influencia fuese negativa, o sea que a un incremento de A le seguirá una disminución de B y viceversa, y se representa:
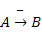
De este modo, asociando un signo a las relaciones de influencia, se tiene un diagrama de carácter cualitativo que suministra una valiosa información sobre la estructura del sistema. En la Ilustración 5 se muestra el diagrama de llenar un vaso con agua, mediante un grafo de este tipo.
 |
Siendo la interpretación de la ilustración 5, la siguiente:
- si aumenta la discrepancia con el nivel deseado, aumenta el flujo de agua;
- si aumenta el flujo de agua, aumenta el nivel;
- si aumenta el nivel, disminuye la discrepancia.
Estructura de realimentación
Una estructura básica en el estudio del comportamiento de un sistema es la estructura de realimentación. La realimentación nos va a proporcionar una transmisión de información circular de forma continua. Esta estructura circular aparece en muchas situaciones y está en el origen de comportamientos complejos en donde la discrepancia entre el estado y objetivo determina la acción que modifica el estado en el sentido de que alcance el objetivo deseado (que la discrepancia se anule).
El comportamiento asociado a los bucles de realimentación, son modos de comportamiento que cabe imputar a la estructura del sistema, y no a las partes que lo forman. En este sentido decimos que los bucles de realimentación son elementos básicos para la generación endógena del comportamiento.
Bucle de realimentación negativa
El diagrama de un bucle de realimentación negativa aporta el esquema básico de todo comportamiento orientado a un objetivo; su propiedad característica hace que, si alguno de sus elementos es perturbado por alguna acción exterior, el sistema, en virtud de su estructura, reacciona tendiendo a anular esa perturbación.
Consideremos el bucle de la Ilustración 6, en el que los elementos se han representado, de forma general, mediante las letras A, B, y C.
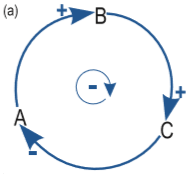 |
Del grafo podemos deducir que:
- si el elemento B se incrementa, implicará el incremento de C, ya que la relación de influencia correspondiente es positiva,
- el incremento de C implicará el decrecimiento de A, por el carácter negativo de la influencia, y
- el decrecimiento de A dará lugar al decrecimiento de B, pues la relación es positiva; lo que indica que es en el mismo sentido.
Por tanto, el incremento inicial de B le «vuelve», a lo largo de la cadena de realimentación, como un decremento; es decir, la propia estructura de realimentación tiende a anular la perturbación inicial, que era un incremento, generando un decremento. De este modo se comprende que los bucles de realimentación negativa son bucles estabilizadores, que tienden a anular las perturbaciones exteriores.
Los bucles de realimentación negativa son bucles que estabilizan los sistemas; están para brindar la información que se precisa en la toma de decisiones a fin de realizar las acciones pertinentes para que los resultados se ajusten a los objetivos planeados.
Bucle de realimentación positiva
En un bucle de retroalimentación positiva, todas las influencias son positivas, y si las hubiese negativas, se han de compensar por pares.
En la Ilustración 7 se representa de forma esquemática, mediante las letras A, B y C, un bucle de esta naturaleza. Con ayuda de este diagrama se puede analizar, de forma general, el comportamiento que genera este bucle. Si cualquiera de sus elementos sufre una perturbación, ésta se propaga, reforzándose, a lo largo del bucle.
 |
En este caso,
- si A se incrementa, entonces B se incrementa,
- dado el incremento de B, C se incrementa, y consecuentemente
- al C incrementarse, A se incrementa.
Por lo tanto, la propia estructura del sistema determina que el crecimiento inicial de 'A' «vuelva» reforzado a 'A', iniciándose de este modo un proceso sin fin que determinará el crecimiento de 'A'.

Este efecto donde el cambio se amplifica produciendo más cambio, también se conoce con el nombre de «bola de nieve». Se trata, por tanto, de una realimentación que amplifica las perturbaciones y que, por tanto, inestabiliza al sistema.
Retrasos
Hemos visto como la información sobre las relaciones de influencia podía enriquecerse con la adición de un signo. Ahora nos interesa, además, distinguir entre influencias que se producen de forma instantánea e influencias que tardan un cierto tiempo en manifestarse. En este último caso, se tienen influencias a las que se asocian retrasos. En el diagrama de influencias, si A influye sobre B, y esta influencia tarda un cierto tiempo en manifestarse, entonces se añaden dos trazos sobre la flecha correspondiente. En la Figura 9a se muestra un bucle de realimentación negativa en el que la influencia entre C y A se produce con un retraso, por lo que la flecha correspondiente presenta dos trazos.
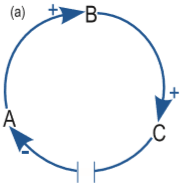 |
Los retrasos tienen una influencia en el comportamiento de un sistema, a saber:
- En los bucles de realimentación positiva determinan que el crecimiento no se produzca a la velocidad esperada.
- En los bucles de realimentación negativa su presencia implica una oscilación del sistema.
Así en la Figura 9b se muestra el posible comportamiento del sistema de la Figura 9a, en el que se produce una oscilación en torno al objetivo. Precisamente, el análisis de estas oscilaciones en una empresa con retrasos en la transmisión de información se encuentra en los orígenes de la dinámica de sistemas.
 |
Sistemas complejos y estructuras genéricas
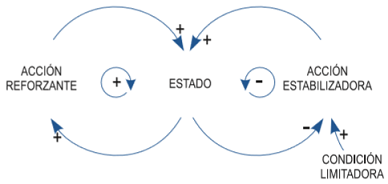
Los bucles de realimentación positiva y negativa constituyen las estructuras más elementales de un sistema que son capaces de generar un comportamiento de forma autónoma. Sin embargo, los sistemas con los que habitualmente nos encontramos son sistemas complejos en los que coexistan múltiples bucles de realimentación. Un ejemplo de un sistema con varios bucles de realimentación es el que se muestra en la Ilustración 10, en el que se tiene una estructura en la que coexisten un bucle de realimentación positiva con uno negativo.
Se trata de procesos en los que inicialmente se produce un crecimiento; es decir, al principio el bucle de realimentación positiva es el dominante luego se incorpora un bucle de realimentación negativa. Cuando el estado ha alcanzado un considerable nivel de crecimiento, como consecuencia de que el bucle de realimentación positiva es dominante, se invierte la dominancia de los bucles, de modo que el nuevo bucle dominante es el negativo y se produce la limitación del crecimiento.
 |
| . |
Todo sucede al combinarse el crecimiento asociado a un bucle de realimentación positiva, en la fase inicial del proceso, con el comportamiento asintótico correspondiente a un bucle de realimentación negativa, en la fase terminal.
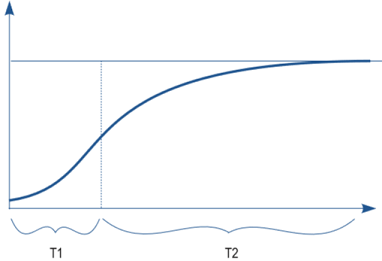
En la Ilustración 11 se muestra la combinación de estos dos modos de comportamiento, que da lugar a la conocida curva de crecimiento sigmoidal o logística. La estructura de la Ilustración 10 permite dar una interpretación estructural del comportamiento que aparece en la Ilustración 11, y así vemos cómo es posible asociar estructura y comportamiento, que es el objetivo fundamental de la dinámica de sistemas.
 |
El número de procesos a los que se puede aplicar esta estructura de dos bucles es muy amplio y comprende desde la introducción de un nuevo producto en un mercado (con una fase inicial de implantación y gran crecimiento, y una fase final de saturación) hasta la introducción de una nueva población en un hábitat en el que inicialmente estaba ausente.
La estructura que se ha representado en la Ilustración 10 constituye un ejemplo de lo que se conoce como arquetipos sistémicos o estructuras genéricas. Se trata de situaciones típicas que aparecen en problemas muy variados, pero que admiten la misma descripción básica desde un punto de vista sistémico. Aquí hemos presentado una de las más sencillas, pero en la literatura se encuentra un gran número de ellas. Una presentación más completa de los arquetipos sistémicos puede verse en el libro titulado La quinta disciplina de Peter Senge (Senge, 2010 ).
Seguidamente se presentarán instrumentos de la dinámica de sistemas que permiten elaborar los diagramas de influencias para convertirlos en objetos matemáticos, que programados con aplicaciones informáticas permitirán generar las trayectorias que representan el comportamiento de los sistemas.
De la estructura al comportamiento: diagramas de Forrester
La estructura de un sistema puede tener un carácter esencialmente estático o dinámico. Ahora para dilucidar su comportamiento, se puede partir de la observación de distintos elementos que aparecen en los nodos de un diagrama de influencias, y determinar si algunos de ellos representan variaciones con respecto al tiempo de otras magnitudes consideradas en ese mismo diagrama. Por ejemplo, en el diagrama de la Ilustración 5 -Diagrama de influencias con signos del proceso de llenar un vaso- la variable 'Flujo de agua' representa la variación con respecto al tiempo del nivel alcanzado por el fluido en el vaso. Recordando esa figura se tiene:
Flujo → Nivel |
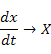 |
En donde:
 denota la variación de la magnitud 'X' con respecto al tiempo 't',
denota la variación de la magnitud 'X' con respecto al tiempo 't',- la variable
 se denomina: variable de flujo, y
se denomina: variable de flujo, y - la variable 'X' se denomina: variable de nivel o variable de estado o nivel.
Forrester postula una clasificación de las distintas variables que aparecen en un diagrama de influencias en tres grupos:
- variables de nivel o estado,
- variables de flujo, y
- variables auxiliares.
Las variables de nivel o estado son normalmente las variables más importantes y representan esas magnitudes cuya evolución es especialmente significativa. Asociada a cada variable de estado se encuentran una o varias variables de flujo, que determinan su variación a lo largo del tiempo. Por último, las variables auxiliares son el resto de las variables que aparecen en el diagrama, y representan pasos intermedios para la determinación de las variables de flujo a partir de las variables de nivel.
Por tanto, una vez clasificados los elementos que aparecen en el diagrama de influencias o diagrama causal en variables de: nivel, flujo, y auxiliares estamos en condiciones de elaborar el diagrama de Forrester (o diagrama de flujos y niveles), en donde las variables de nivel, flujo y auxiliares se asocian básicamente como se muestra en la Ilustración 12.
En la siguiente Tabla 1, se muestran todos los símbolos utilizados originalmente en los diagramas de Forrester.
Tabla 1 Símbolos del diagrama de Forrester o diagrama de flujos y niveles.

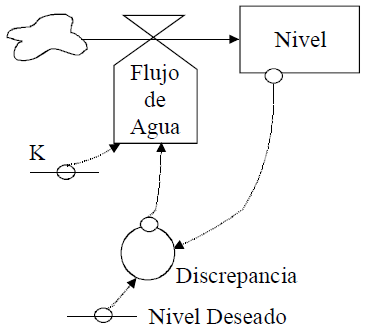
En la Ilustración 12 se tiene el diagrama de Forrester del proceso de llenar un vaso, particularizando los elementos que aparecen en el de la Ilustración 5 Diagrama de influencias con signos del proceso de llenar un vaso-, convirtiendo cada uno de ellos en una variable: de estado, de flujo, o auxiliar, según corresponda y en donde:
- 'Nivel' es una 'variable de estado o nivel',
- 'Flujo de Agua' es una 'variable de flujo',
- 'Discrepancia' es una 'variable auxiliar', ya que representa un paso intermedio en la determinación de 'Flujo de Agua',
- la 'constante K' representa la proporción de agua que se deja pasar en función de la 'Discrepancia' existente, y
- la 'constante Nivel Deseado'
 |
Seguidamente, se muestra cómo se asocian al diagrama de Forrester, las respectivas ecuaciones funcionales. Por ejemplo, para nuestro caso, consideramos la relación entre la variable 'Flujo de Agua' (FA) y la variable 'Nivel' (N). La evolución de esta variable de estado 'Nivel' (N) viene dada por la expresión:
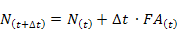
que indica que el 'Nivel' (N) en el instante de tiempo 't + ∆t' se obtiene sumando al 'Nivel' que existía en el tiempo 't' el 'Flujo de Agua' (FA) que se ha producido en el periodo de tiempo entre 't' y 't + ∆t'. La ecuación anterior recibe la denominación de ecuación de estado, e indica cómo evoluciona la variable de estado N en función del 'Flujo de Agua' (FA) que determina su variación. Esta ecuación, también se puede escribir empleando notación diferencial:
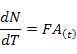
El 'Flujo de Agua' (FA) se determina con ayuda de la expresión:

Esta ecuación, que se denomina «ecuación de flujo», establece que el 'Flujo de Agua' (FA) se obtiene multiplicando la 'Constante K' (K) por la 'Discrepancia' (D); donde K representa la proporción de agua que se deja pasar en función de la 'Discrepancia' (D) existente.
La variable auxiliar 'Discrepancia' (D), viene dada por:

En el modelo, se puede observar que han aparecido dos parámetros: ND y K. En general, para que el modelo se refiera a una situación concreta, a los parámetros hay que darles un valor numérico.
Ello se hace habitualmente de dos maneras:
- se entiende el significado concreto de esos parámetros, y se dispone de información numérica suficiente para conocer sus valores, o bien
- en los casos en los que no se disponga de información sobre los valores de los parámetros, pero sin embargo se disponga de datos con relación a la evolución de las magnitudes significativas del sistema en un periodo de tiempo determinado, se pueden emplear técnicas de ajuste de parámetros. Estas técnicas consisten, esencialmente, en determinar los valores numéricos de los parámetros que minimizan algún índice que mida la discrepancia entre los datos históricos de evolución del proceso y los generados por el sistema dinámico.
Entonces, las «ecuaciones de flujo» permiten determinar una variable de flujo a partir de determinados parámetros del modelo (en este caso K), de variables auxiliares (como D) o de variables de estado (Nivel).
Con el diagrama de Forrester y con la escritura de las ecuaciones del modelo, la información que se ha considerado en los mismos es de naturaleza cualitativa. Hasta el momento en el ejemplo que venimos trabajando, se muestran los elementos básicos en la descripción de un sistema; lo que precisamos ahora, es de la información cuantitativa para asignar valores numéricos a los parámetros que intervienen en esas expresiones; para ello la función tabla que nos permitirá representar las dependencias no lineales entre variables. Por ejemplo, supongamos que la variable auxiliar B es función de A, mediante una expresión de la forma B = f(A). Supongamos que la función f tiene la forma que se indica en la Ilustración 13.
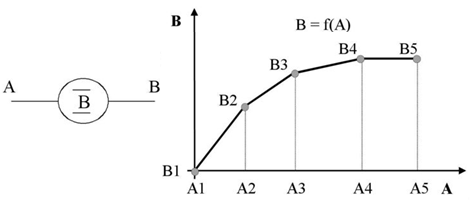 |
Es habitual que esta función se dé, mediante una tabla de valores correspondientes a determinados valores de A (por ello la denominación de función de tabla). En un diagrama de Forrester se representa mediante un círculo tal como se indica en la Ilustración 13.
Hasta aquí hemos completado el proceso mediante el cual, a partir de un diagrama de influencias, se puede obtener el diagrama de Forrester, y con él podemos elaborar un objeto matemático que se constituya en un sistema dinámico.
Referencias
Aracil, J. (1995). Dinámica de sistemas. Madrid: ISDEFE.
Senge, P. (2010 ). La quinta disciplina: Cómo impulsar el aprendizaje en la organización inteligente. Buenos Aires: Ediciones Granica .
Recomendaciones
Complementar el marco teórico con:
Condiciones de utilización
Aprobado: 20 de enero de 2020. por Ciencia y Técnica Administrativa
Publicado el 27 de enero de 2020 por: Ciencia y Técnica Administrativa – CyTA
Pte. Tte. Gral. Perón 3047 PB.3, Buenos Aires Argentina
Copyright © 2020 por Ciencia y Técnica Administrativa
Todos los derechos reservados bajo las convenciones internacionales y panamericanas de derecho de autor, para fines no comerciales.
Esta publicación puede ser reproducida o transmitida en cualquier forma o por cualquier medio sin permiso previo escrito por el editor, siempre que: se reproduzca con precisión, se identifique la fuente del material, y se reconozca el estado de Copyright © Ciencia y Técnica Administrativa - CyTA.
Series de estándares de información nacional
CyTA / Leva bajo norma Niso Z39.18-2005 (Revisión 2010)