 Características
de la distribución F
Véalo
aquí
Existe una “familia” de distribuciones F.
Cada miembro de la familia está determinado por dos parámeteros:
los grados de libertad (gl) en el numerador y los grados de
libertad en el denominador.
El valor de F no puede ser negativo y es una distrubución
continua.
La distribución F tiene sesgo postivo.
Sus valores varían de 0 a ¥ . Con forme
F ® ¥
la curva se aproxima al eje X.
Prueba para variancias iguales
Véalo
aquí
Para prueba de dos colas, el estadístico de prueba está dado
por:
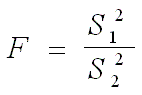
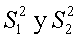 son
las variancias muestrales para las dos muestras. La hipótesis nula
se rechaza si el cálculo del estadístico de prueba es más grande
que el valor crítico (de tablas) con nivel de confianza
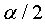 y
grados de libertad para el numerador y el denominador.
Ejemplo:
Colin, agente de bolsa del Critical Securities, reportó que la
tasa media de retorno en una muestra de 10 acciones de software
fue 12.6% con una desviación estándar de 3.9%. La tasa media de
retorno en una muestra de 8 acciones de compañías de servicios fue
10.9% con desviación estándar de 3.5%. Para .05 de nivel de
significancia, ¿puede Colin concluir que hay mayor variación en
las acciones de software?
Paso 1:
Paso 2: H0 se rechaza si F > 3.68,
gl = (9, 7), a= .05
Paso 3:
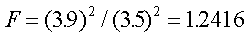
Paso 4: H0 no se rechaza. No hay evidencia suficiente para
asegurar que hay mayor variación en las acciones de software.
Suposiciones de ANOVA
Véalo
aquí
La distribución F también se usa para probar la igualdad de
más de dos medias con una técnica llamada análisis de variancia (ANOVA).
ANOVA requiere las siguientes condiciones:
la población que se muestrea tiene una distribución normal
las poblaciones tienen desviaciones estándar iguales
las muestras se seleccionan al azar y son independientes
Estadísticas
Inferencial
Véalo
aquí
Estadística inferencial: una decisión, estimación,
predicción o generalización sobre una población, en base a una
muestra.
Una población es un conjunto de todos los posibles
individuos, objetos o medidas de interés.
Una muestra es una porción, o parte, de la población de
interés.
Procedimiento
de análisis de variancia
Véalo
aquí
Hipótesis nula: las medias de las poblaciones son iguales.
Hipótesis alterna: al menos una de las medias es diferente.
Estadístico de prueba: F = (variancia entre muestras)/(variacia
dentro de muestras).
Regla de decisión: para un nivel de significancia , la hipótesis
nula se rechaza si F (calculada) es mayor que F (en tablas) con
grados de libertad en el numerador y en el denominator.
NOTA
Véalo
aquí
Si se muestrean k poblaciones, entonces los gl (numerador) = k
- 1
Si hay un total de N puntos en la muestra, entonces los gl
(denominador) = N - k
El estadístico de prueba se calcula con: F = [(SST) /(k - 1)] /[(SSE)
/(N - k)].
SST es la suma de cuadrados de los tratamientos.
SSE es la suma de cuadrados del error.
Sea TC el total de la columna, nc el número de observaciones en
cada columna, y SX la suma de todas las
observaciones.
Fórmulas
Véalo
aquí
Inferencias
acerca de las medias de tratamiento
Véalo
aquí
Cuando se rechaza la hipótesis nula de que las medias son
iguales, quizá sea bueno saber qué medias de tratamiento difieren.
Uno de los procedimientos más sencillo es el uso de los intervalos
de confianza.
Intervalos
de confianza para la diferencia entre dos medias
Véalo
aquí
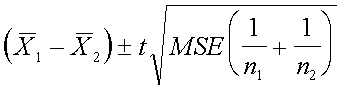donde t se obtiene de la tabla con (N - k) grados de libertad.
MSE = [SSE /(N - k)]
Dos
factores ANOVA
Véalo
aquí
Para ANOVA de dos factores se prueba si existe una diferencia
signifcativa entre el efecto de tratamiento y si existe una
diference en la variable de bloqueo.
Sea Br el total de bloque (r según las filas)
SSB representa la suma de los cuadrados de los bloques, donde:
|
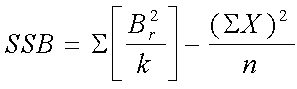
