|
|
|
 Características
de la distribución t de Student
Véalo
aquí
La distribución t tiene las siguientes propiedades:
es continua, tiene forma de campana y es simétrica respecto al
cero como la distribución z.
existe una familia de distribuciones t que comparten una media de
cero pero con desviaciones estándar diferentes.
la distribución t está más dispersa y es más plana en el centro
que la distribución z, pero se acerca a ella cuando el tamaño de
la muestra crece.
Prueba para la media poblacional: muesra pequeña, desviación
estándar poblacional desconocida
Vealo
aquí
NOTA
Véalo
aquí
Para una prueba de dos colas con la distribución t, se rechaza
la hipótesis nula cuando el valor del estadístico de prueba es
mayor que
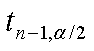
o si es menor que -
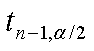
Para una prueba de cola izquierda con la distribución t, se
rechaza la hipótesis nula cuando el valor del estadístico de
prueba es menor que
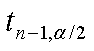
Comparación
de dos medias poblacionales
Véalo
aquí
Para realizar esta prueba se requieren tres suposiciones:
las poblaciones deben tener una distribución normal o normal
aproximada
las poblaciones deben ser independientes
las variancias de las poblaciones deben ser iguales
Variancia
muestral combinada y estadístico de prueba
Véalo
aquí
Variancia muestral combinada:
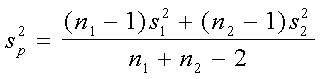
Estadístico de prueba:
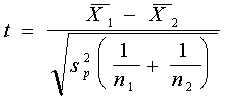Un estudio EPA reciente compara la economía de combustible en
carretera de los automóviles nacionales e importados. Una muestra
de 15 autos nacionales reveló una media de 33.7 mpg con desviación
estándar de 2.4 mpg. Una muestra de 12 autos importados indicó una
media de 35.7 mpg con desviación estándar de 3.9. Para .05 de
nivel de significancia, ¿puede EPA concluir que el consumo de las
mpg para los autos importados es mayor? (Asocie el subíndice 1 con
los autos nacionales.)
Paso 1:
Paso 2: H0 se rechaza si t<-1.708, gl=25
Paso 3: t=1.64 (verifique)
Paso 4: H0 no se rechaza. La evidencia muestral es insuficiente
para asegurar que el consumo de mpg es más alto en los autos
importados.
Pruebas
de hipótesis con observaciones por pares
Véalo
aquí
Las muestras independientes que no están relacionadas.
Las muestras dependientes están pareadas o relacionadas de alguna
manera.
Por ejemplo, si se desea comprar un auto se busca el mismo modelo
en dos (o más) distribuidores diferentes y se comparan los
precios.
Use la siguiente prueba cuando las muestras son dependientes:
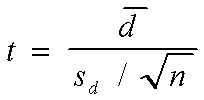donde es el promedio de las diferencias
es la desviación estándar de las diferencias
n es el número de pares (diferencias)
Ejemplo:
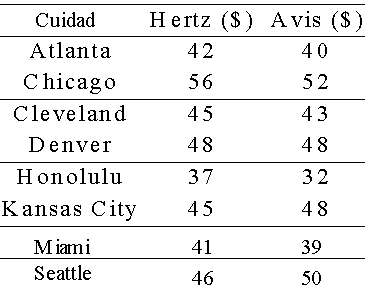
Una empresa independiente de pruebas estadísticas compara el
costo diario de renta de un auto compacto en Hertz y en Avis. Se
obtiene una muestra aleatoria de ocho ciudades con la siguiente
información. Para .05 de nivel de significancia, ¿puede la empresa
de pruebas concluir que existe una diferencia en los costos de
renta?
Paso 1:
Paso 2: H0 se rechaza si t<-2.365 o t>2.365
Paso 3:
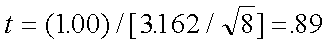
Paso 4: H0 no se rechaza. No existe diferencia en los costos.
Variables
Cuantitativas Discretas
Véalo
aquí
Variables discretas: sólo pueden adquirir ciertos
valores y casi siempre hay “brechas” entre esos valores.
EJEMPLO: el número de habitaciones en un hotel (1,2,3,....).
Variables
Cuantitativas Continuas
Véalo
aquí
Variables continuas: pueden tomar cualquier valor
dentro de un intervalo específico.
EJEMPLO: el tiempo que toma volar de Buenos Aires a Bogotá.
Niveles
de medición
Véalo
aquí
Nivel nominal: los datos sólo se puede clasificar en
categorías, no se pueden ordenar.
EJEMPLOS: color de los ojos, sexo, afiliación religiosa.
Mutuamente excluyente: un individuo, objeto o artículo,
al ser incluido en una categoría, debe excluirse de las demás.
EJEMPLO: color de los ojos.
Exhaustivo: cada persona, objeto o hecho debe clasificarse
al menos en una categoría.
EJEMPLO: afiliación religiosa.
Nivel ordinal: involucra datos que se pueden ordenar,
pero no es posible determinar las diferencias entre los valores de
los datos o no tienen significado.
EJEMPLO: en una prueba de sabor de 4 refrescos de cola, el C se
clasificó como número 1, el B como número 2, el A como 3 y el D
como número 4.
Nivel de intervalo: similar al nivel ordinal, con la
propiedad adicional de que se pueden determinar cantidades
significativas de las diferencias entre los valores. No existe un
punto cero natural.
EJEMPLO: temperatura en la escala de grados Fahrenheit.
Nivel de razón: el nivel de intervalo con un punto cero
inicial inherente. Las diferencias y razones son significativas
para este nivel de medición.
EJEMPLOS: dinero, altura de los jugadores de basquetbol de la NBA.
|
|
