 ¿Qué
es una hipótesis?
Véalo
aquí
Hipótesis: enunciado acerca de una población elaborada con el
propósito de ponerse a prueba.
Ejemplos de hipótesis acerca de un parámetro de población son:
la media mensual de ingresos para analistas de sistemas es $3625,
el 20% de los delincuentes juveniles son capturados y sentenciados
a prisión.
¿Qué es una prueba de hipótesis?
Vealo
aquí
Prueba de hipótesis: procedimiento basado en la evidencia
muestral y en la teoría de probabilidad que se emplea para
determinar si la hipótesis es un enunciado razonable y no debe
rechazarse o si no es razonable y debe ser rechazado.
Prueba de hipótesis
Véalo
aquí
Definiciones
Véalo
aquí
Hipótesis nula H0: afirmación acerca del valor de un
parámetro poblacional.
Hipótesis alterna H1: afirmación que se aceptará si los
datos muestrales proporcionan evidencia de que la hipótesis nula
es falsa.
Nivel de significancia: probabilidad de rechazar la
hipótesis nula cuando es verdadera.
Error Tipo I: rechazar la hipótesis nula cuando en realidad
es verdadera.
Error Tipo II: aceptar la hipótesis nula cuando en realidad
es falsa.
Estadístico de prueba: valor obtenido a partir de la información
muestral, se utiliza para determinar si se rechaza o no la
hipótesis.
Valor crítico: el punto que divide la región de aceptación
y la región de rechazo de la hipótesis nula.
Prueba
de significancia de una cola
Véalo
aquí
Una prueba es de una cola cuando la hipótesis alterna, H1,
establece una dirección, como:
H0 : el ingreso medio de las mujeres es menor o igual
al ingreso medio de los hombres.
H1 : el ingreso medio de las mujeres es mayor que el de
los hombres.
Distribución de muestreo para el valor estadístico z, prueba
de una cola, nivel de significancia de .05
Prueba
de significancia de dos colas
Véalo
aquí
Una prueba es de dos colas cuando no se establece una
dirección específica de la hipótesis alterna H1, como:
H0 : el ingreso medio de las mujeres es igual al ingreso
medio de los hombres.
H1 : el ingreso medio de las mujeres no es igual al ingreso
medio de los hombres.
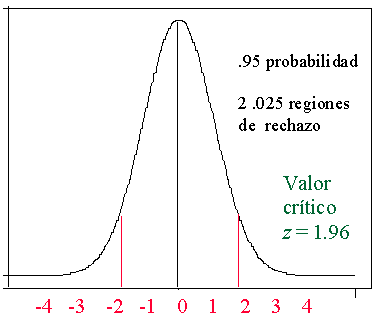
Distribución de muestreo para el valor estadístico z,
prueba de dos colas, nivel de significancia de 0.05
Prueba
para la media poblacional: muestra grande, desviación estándar
poblacional conocida
Véalo
aquí
Cuando se hace una prueba para la media poblacional de una
muestra grande y se conoce la desviación estándar, el estadístico
de prueba está dado por:
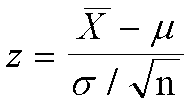Los fabricantes de Fries’ Catsup indican en su etiqueta que el
contenido de la botella es de 16 onzas. Cada hora se toma una
muestra de 36 botellas y se pesa el contenido. La muestra de la
última hora tiene un peso medio de 16.12 onzas con una desviación
estándar de .5 onzas. ¿Está el proceso fuera de control para un
nivel de significancia de .05?
Paso 1: establezca la hipótesis nula y alterna
Paso 2: establezca la regla de decisión:
Paso 3: calcule el valor del estadístico de prueba:
H0 se rechaza si z <- 1.96 o z > 1.96
Paso 4: decisión sobre H0: no se rechaza H0
porque 1.44 es menor que el valor crítico 1.96
Valor
p en la prueba de hipótesis
Véalo
aquí
Valor p: es la probabilidad de observar un valor muestral tan
extremo o más que el valor observado, dado que la hipótesis nula
es verdadera.
Si el valor p es menor que el nivel de significancia, H0 se
rechaza.
Si el valor p es mayor que el nivel de significancia, H0 no se
rechaza.
Cálculo
del valor p
Véalo
aquí
Prueba de una cola:
valor p = P { z el valor absoluto del estadístico de prueba
calculado}
Prueba de dos colas:
valor p = 2P { z el valor absolut del estadístico de prueba
calculado}
Para el primer ejemplo,
z = 1.44, y para una prueba de dos colas, el valor p = 2P { z
1.44} = 2(.5-.4251) = .1498. Como .1498 > .05, no se rechaza H0.
Prueba
para la media poblacional: muestra grande, desviación estándar
poblacional desconocida
Véalo
aquí
Aquí σ es desconocida, así que se estimará con la desviación
estándar de la muestra s.
Siempre que el tamaño de muestra n ³30,
z puede aproximarse con:
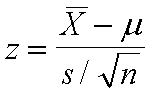Ejemplo:
La cadena Roder’s Discount emite su propia tarjeta de crédito.
Lisa, la gerente de crédito, quiere encontrar si la media mensual
de saldos no pagados es mayor que $400. El nivel de significancia
es de .05. Una revisión al azar de 172 saldos reveló que la media
muestral es $407 y la desviación estándar muestral es $38. ¿Debe
Lisa concluir que la población media es mayor que $400, o es
razonable suponer que la diferencia de $7 ($407-$400) se debe al
azar?
Paso 1:
Paso 2: H0 se rechaza si z > 1.645
Paso 3:
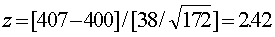
Paso 4: H0 se rechaza. Lisa puede concluir que la media de saldos
no pagados es mayor que $400.
.
Prueba
de hipótesis: dos medias poblacionales
Véalo
aquí
Suponga que los parámetros para dos poblaciones son:
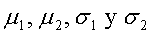
Para muestras grandes el estadístico de prueba es:
Cuando σ1 y σ2 no se conocen pero el tamaño de muestra n1 y n2
es mayor o igual que 30, el estadístico de prueba es
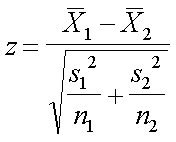
Ejemplo:
Se realizó un estudio para comparar los años promedio de
servicio de quienes se retiraron en 1979 con los que se retiraron
el año anterior en Delong Manufacturing Co. Con un nivel de
significancia de .01 ¿podemos concluir que los trabajadores que se
retiraron el año pasado trabajaron más años según la siguiente
muestra? Nota: sea población #1= año anterior.
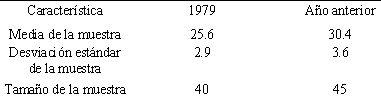
Paso 1:
Paso 2: Rechace H0 si z > 2.33
Paso 3:
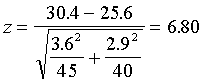
Paso 4: Como z = 6.80 > 2.33, H0 se rechaza. Los que se retiraron
el año anterior tenían más años de servicio.
Pruebas
respecto a relaciones proporcionales
Véalo
aquí
Relación proporcional: parte fraccional o porcentaje que
indica la parte de la población o muestra que tiene un atributo
particular de interés.
La relación proporcional muestral se representa por
`R donde
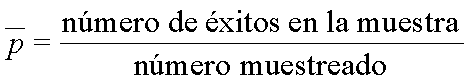
Estadístico
de prueba para ensayos con una sola relación proporcional de
población
Véalo
aquí
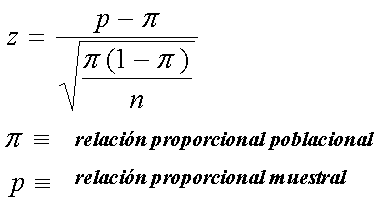Ejemplo:
En el pasado, 15% de la propaganda por correo para donativos
dio como resultado contribuciones. Se mandó una nueva carta a una
muestra de 200 personas y 45 enviaron un donativo. Para .05 de
significancia, ¿se puede concluir que la nueva carta fue más
efectiva?
Paso 1:
Paso 2: H0 se rechaza si z > 1.645
Paso 3:
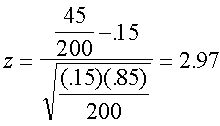
Paso 4: como z = 2.97 >1.645, H0 se rechaza. La nueva carta es más
efectiva.
Prueba
donde interviene la diferencia entre dos relaciones proporcionales
de población
Véalo
aquí
El estadístico de prueba en este caso es:
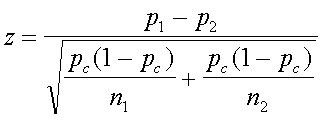
Ejemplo:
¿Es más probable que los trabajadores solteros falten más que
los trabajadores casados?
Una muestra de 250 trabajadores casados indicó que 22 faltaron
más de 5 días el año pasado, mientras que una muestra de 300
trabajadores solteros indicó que 35 faltaron más de 5 días.
Utilice .05 de nivel de significancia.
Nota: sea población #1 = trabajadores solteros.
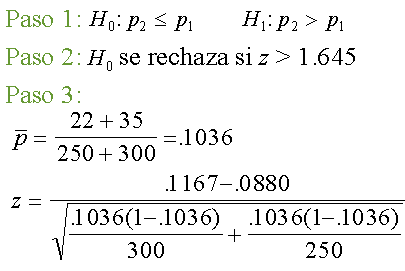Paso 4: H0 no se rechaza. No existe diferencia entre la
proporción de trabajadores casados y solteros que faltan más de 5
días al trabajo.
El valor p = P{ z > 1.1} = .1357
|
