 ¿Por
qué obtener muestras de la población?
Véalo
aquí
Existe una imposibilidad física de verificar todos los
elementos de la población.
El costo de estudiar todos los elementos de una población es alto.
Los resultados de la muestra suelen ser adecuados.
Contactar a toda la población es tardado, por la naturaleza
destructiva de ciertas pruebas.
Muestra aleatoria
Véalo
aquí
Una muestra aleatoria es una muestra seleccionada de manera
que cada elemento o persona en la población que se estudia tiene
una probabilidad conocida de quedar incluido en la muestra.
Métodos de muestreo aleatorio
Véalo
aquí
Muestra aleatoria simple: muestra formulada de manera
que cada elemento o persona en la población tiene la misma
oportunidad de quedar incluida.
Muestra aleatoria sistemática: los artículos o individuos
de la población se colocan en cierto orden. Se elige un punto de
partida aleatorio y después se selecciona uno cada
k-ésimo elemento de la población para la muestra.
Muestreo aleatorio estratificado: se divide la
población en subgrupos, llamados estratos, y se selecciona una
muestra de cada estrato.
Muestreo por conglomeración: primero se divide la población
en subgrupos (estratos), y se selecciona un estrato. La muestra se
toma del estrato seleccionado.
El error de muestreo es la diferencia entre un estadístico
muestral y su parámetro correspondiente.
.
Distribución
de muestreo de medias muestrales
Véalo
aquí
La distribución de muestreo de medias muestrales es la
distribución de probabilidad de todas la medias muestrales
posibles de un tamaño de muestra dado, seleccionadas de una
población, y la probabilidad de ocurrencia asociada con cada media
muestral.
Ejemplo:
El despacho de abogados Hoya & Associados tiene cinco socios.
En su junta de socios semanal cada uno informa el número de
horas que cobraron a los clientes por sus servicios la semana
anterior.
|
Socio |
Horas |
| Giordanino |
22 |
| Barnabá |
26 |
| Torres |
30 |
| Carrizo |
26 |
| Salgado |
22 |
Si se seleccionan al azar dos socios, ¿cuántas muestras
diferentes son posibles?.
Organice las medias muestrales en una distribución de muestreo.
| Media
Muestral |
Frecuencia |
Frecuencia
relativa |
| 22 |
1 |
1/10 |
| 24 |
4 |
4/10 |
| 26 |
3 |
3/10 |
| 28 |
2 |
2/10 |
Calcule la media de las medias muestrales y compárela con la
media poblacional:
media de las medias muestrales
= [(22)(1) + (24)(4) + (26)(3) + (28)(2)]/10=25.2
media poblacional = (22+26+30+26+22)/5 = 25.2
observe que la media de las medias muestrales es igual a la
media poblacional.
Teorema
del límite central
Véalo
aquí
Para una población con media σ y variancia σ 2,
la distribución de muestreo de las medias de todas las muestras
posibles de tamaño n obtenidas de una población tendrá una
distribución normal aproximada —con la media de la distribución de
muestreo igual a σ y la variancia igual a σ
2/ n —si se supone que el tamaño de la muestra es
suficientemente grande.
Estimaciones
puntuales
Véalo
aquí
Una estimación puntual es un valor (punto) que se usa para
estimar un parámetro de la población.
Ejemplos de estimaciones puntuales son media muestral, desviación
estándar muestral, variancia muestral, relación proporcinal de la
muestra, ...
EJEMPLO 2: se registra el número de defectos producidos durante 5
horas seleccionadas al azar en una semana de 40 horas. Los
defectos observados fueron 12, 4, 7, 14 y 10. La media muestral es
9.4. Entonces la estimación puntual para el promedio de defectos
por hora es 9.4.
Estimaciones
de intervalo
Véalo
aquí
Una estimación de intervalo establece la amplitud en la que
quizá se encuentre un parámetro poblacional.
El inervalo dentro del cual se espera que esté un parámetro
poblacional se llama intervalo de confianza.
Los dos intervalos de confianza que más se usan son 95% y 99%.
Un intervalo de confianza de 95% significa que cerca de 95% de
los intervalos similares contendrán el parámetro que se quiere
estimar, o 95% de las medias muestrales para un tamaño de muestra
dado estarán dentro de 1.96 deviaciones estándar de la media
poblacional hipotética.
Para el intervalo de confianza de 99%, un 99% de las medias
muestrales para un tamaño de muestra dado estará dentro de 2.58
desviaciones estándar de la media poblacional hipotética.
Error
estándar de la media muestral
Véalo
aquí
El error estándar de las medias muestrales es la desviación
estándar de la distribución de muestreo de las medias muestrales.
Se calcula mediante
σx es el símbolo del error estándar de las medias muestrales.
σ es la desviación estándar de la población.
n es el tamaño de la muestra.
Si σ no se conoce y n σ 30, la desvición estándar de la
muestra, denotada por s, se usa para aproximar la desviación
estándar poblacional. La fórmula para el error estándar se
convierte en:
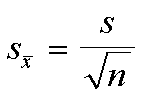
Intervalos
de confianza de 95% y 99% para µ
Véalo
aquí
Los intervalos de confianza de 95% y 99% para μ cuando n
³ 30 se forman como sigue:
el IC de 95% para la media poblacional está dado por
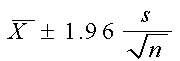
el IC de 99% para la media poblacional está dado por
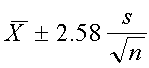
Construcción
general de IC para µ
Véalo
aquí
En general, un intervalo de confianza para la media se calcula
mediante:
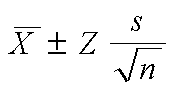
Ejemplo:
El director de la escuela de administración desea estimar el
número medio de horas por semana que estudian los alumnos. Una
muestra de 49 estudiantes dio una media de 24 h con desviación
estándar de 4 h.
La estimación puntual es 24 h (media muestral).
¿Cuál es el intervalo de confianza de 95% para el número promedio
de horas por semana que estudian los alumnos?
Si se usa un IC de 95% para la media poblacional, se tiene
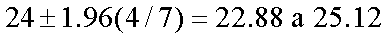
Los puntos terminales del intervalo de confianza son los límites
de confianza. El límite inferior de confianza es 22.88 y el límite
superior de confianza es 25.12
Intervalo
de confianza para una relación proporcional de población
Véalo
aquí
El intervalo de confianza para una relación proporcional de
una población se estima como:
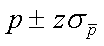
donde es el error estándar de la proporción:
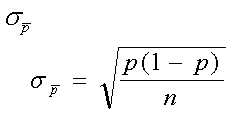
Matt Williams, planificador financiero, estudia los planes de
retiro para jóvenes ejecutivos. Una muestra de 500 ejecutivos que
son dueños de sus casas reveló que 175 planean venderlas y
retirarse en Arizona. Desarrolle un intervalo de confianza de 98%
para la proporción de ejecutivos que planean vender e irse a
Arizona.
Aquí, n=500, p=175/500=.35 y z=2.33
el IC de 98% es
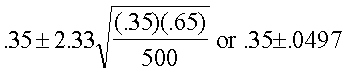
Factor
de corrección de población finita
Véalo
aquí
Se dice que una población con una cota superior fija es
finita.
Para una población finita, donde el número total de objetos es N y
el tamaño de la muestra es n, se hace el siguiente ajuste a los
errores estándar de las medias muestrales y a las proporciones:
Error estándar de las medias muestrales:
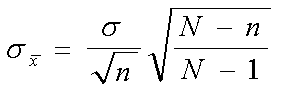
Error estándar de las proporciones de las muestras:
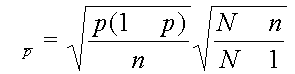
Este adjuste se llama factor de corrección de población finita.
Nota: si n/N < .05, el factor de corrección de población finita se
ignora.
Ejemplo:
Dada la información del EJEMPLO 4, construya un intervalo de
confianza de 95% para el número medio de horas estudiadas por
semana si hay sólo 500 estudiantes en la escuela.
Dado que n/N = 49/500 = .098>.05, se tiene que usar el factor de
corrección de población finita.
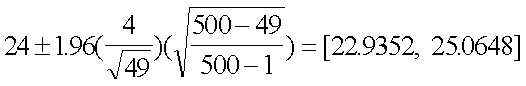
Selección
del tamaño de muestra
Véalo
aquí
Existen 3 factores que determinan el tamaño de una muestra,
ninguno de ellos tiene una relación directa con el tamaño de la
población. Los factores son:
El grado de confianza elegido.
El error máximo permitido.
La variación en la población.
Variación
en la población
Véalo
aquí
Tamaño de la muestra para la media: una fórmula computacional
conveniente para determinar n es:
donde: E es el error permitido, Z es el valor normal estándar
asociado con el grado de confianza seleccionado y S es la
desviación estándar estimada del estudio piloto.
Ejemplo:
Un grupo de consumidores desea estimar la media mensual en los
recibos de luz para una casa unifamiliar. Según estudios similares
la desviación estándar se estima en $20.00. Se desea un nivel de
confianza de 99%, con una precisión de ±$5.00. ¿Qué tamaño de
muestra se requiere?
.
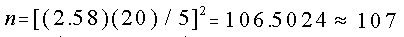
Tamaño
de la muestra para proporciones
Véalo
aquí
La fórmula para determinar el tamaño de la muestra en el caso
de una proporción es:
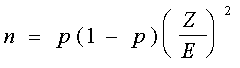
donde p es la proporción estimada, basada en la experiencia o en
un estudio piloto; z es el valor asociado con el nivel de
confianza deseado; E es el error máximo que tolerará el
investigador.
Ejemplo:
El American Kennel Club desea estimar la proporción de niños
que tienen un perro como mascota. Si el club quiere la estimación
dentro de 3% de la relación proporcional, ¿cuántos niños deberán
contactar? Suponga 95% de nivel de confianza y que el club estimó
que 30% de los niños tienen un perro como mascota.
|
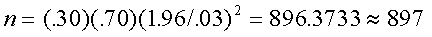
