|
|
|
 Variables
aleatorias Variables
aleatorias
Véalo
aquí
Una variable aleatoria es un valor numérico determinado por el
resultado de un experimento.
Ejemplo: considere un experimento aleatorio en el que se lanza
tres veces una moneda. Sea X el número de caras. Sea H el
resultado de obtener una cara y T el de obtener una cruz.
El espacio muestral para este experimento será: TTT, TTH, THT,
THH, HTT, HTH, HHT, HHH.
Entonces, los valores posibles de X (número de caras) son x = 0,
1, 2, 3.
El resultado “cero caras” ocurrió una vez.
El resultado “una cara” ocurrió tres veces.
El resultado “dos caras” ocurrió tres veces.
El resultado “tres caras” ocurrió una vez.
De la definición de variable aleatoria, la X definida en este
experimento, es una variable aleatoria.
 Distribuciones probabilísticas
Distribuciones probabilísticas
Vealo
aquí
Una distribución probabilística es la enumeración de todos los
resultados de un experimento junto con las probabilidades
asociadas.
Para el Ejemplo anterior,
| Números de caras |
Probabilidad de los
resultados |
| 0 |
1/8 = 0.125 |
| 1 |
3/8 = 0.375 |
| 2 |
3/8 = 0.375 |
| 3 |
1/8 = 0.125 |
| total |
8/8 = 1 |
 Características de una distribución porbabilística
Características de una distribución porbabilística
Véalo
aquí
La probabilidad de un resultado siempre debe estar entre 0 y
1.
La suma de todos los resultados mutuamente excluyentes siempre es
1.
 Variable
aleatoria discreta Variable
aleatoria discreta
Véalo
aquí
Una variable aleatoria discreta es una variable que puede
tomar sólo ciertos valores diferentes que son el resultado de la
cuenta de alguna característica de interés.
EJEMPLO 2: sea X el número de caras obtenidas al lanzar 3 veces
una moneda. Aquí los valores de X son x = 0, 1, 2, 3
Tipos de variables
 Variable
aleatoria continua Variable
aleatoria continua
Véalo
aquí
La media:
indica la ubicación central de los datos.
es el promedio, a la larga, del valor de la variable aleatoria.
también se conoce como el valor esperado, E(x), en una
distribución de probabilidad.
es un promedio ponderado.
La media se calcula con la fórmula:
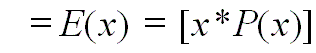
donde μ representa la media y P(x) es la probabilidad de los
diferentes resultados x.
 Variancia
de una distribución probabilística discreta Variancia
de una distribución probabilística discreta
Véalo
aquí
La variancia mide la cantidad de dispersión (variación) de una
distribución.
La variancia de una distribución discreta se denota por la letra
griega σ2 (sigma cuadrada).
La desviación estándar se obtiene tomando la raíz cuadrada de
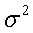 La variancia de una distribución de probabilidad discreta se
calcula a partir de la fórmula
La variancia de una distribución de probabilidad discreta se
calcula a partir de la fórmula
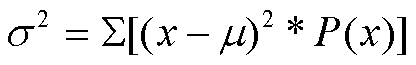 Ejemplo:
Dan Desch, propieatario de College Painters, estudió sus
registros de las últimas 20 semanas y obtuvo los siguientes
números de casas pintadas por semana:
Ejemplo:
Dan Desch, propieatario de College Painters, estudió sus
registros de las últimas 20 semanas y obtuvo los siguientes
números de casas pintadas por semana:
| # de casas pintadas |
semanas |
| 10 |
5 |
| 11 |
6 |
| 12 |
7 |
| 13 |
2 |
Distribución probabilística:
| # de casas pintadas, X |
Probabilidad, P(X) |
| 10 |
0.25 |
| 11 |
0.30 |
| 12 |
0.35 |
| 13 |
0.10 |
| Total |
1 |
Calcule el número medio de casas pintadas por semana:
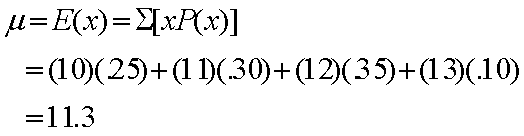
Calcule la variancia del número de casas pintadas por semana:
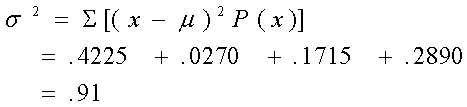
 Distribución
probabilística binomial Distribución
probabilística binomial
Véalo
aquí
La distribución binomial tiene las siguientes características:
un resultado de un experimento se clasifica en una de dos
categorías mutuamente excluyentes -éxito o fracaso.
los datos recolectados son resultados de contar.
la probabilidad de éxito es la misma para cada ensayo.
los ensayos son independientes.
Para elaborar una distribución binomial, sea
n el número de ensayos
x el número de éxitos observados
p la probabilidad de éxito en
cada ensayo
La fórmula para la distribución de probabilidad binomial es:
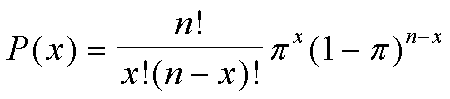 La Secretaría del Trabajo del estado de Alabama reporta que
20% de la fuerza de trabajo en Mobile está desempleada. De una
muestra de 14 trabajadores, calcule las siguientes probabilidades
con la fórmula de la distribución binomial (n=14, =.2, ):
La Secretaría del Trabajo del estado de Alabama reporta que
20% de la fuerza de trabajo en Mobile está desempleada. De una
muestra de 14 trabajadores, calcule las siguientes probabilidades
con la fórmula de la distribución binomial (n=14, =.2, ):
tres están desempleados: P(x=3)=.250
Nota: éstos también son ejemplos de distribuciones
probabilísticas acumulativas:
tres o más están desempleados:
P(x ³3)=.250 +.172 +.086 +.032
+.009 +.002=.551
al menos un trabajador está desempleado:
P(x ³ 1) = 1 - P(x=0) =1 -
.044 = .956
a lo más dos trabajadores están desempleados:
P(x £2)=.044 +.154 +.250 =.448
 Media
y variancia de la distribución binomial Media
y variancia de la distribución binomial
Véalo
aquí
La media está dada por:
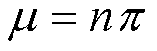
La variancia está dada por:
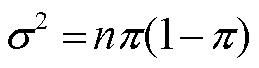 Del ejemplo anterior, recuerde que p=.2
y n=14.
Del ejemplo anterior, recuerde que p=.2
y n=14.
Así, la media = n p = 14(.2) = 2.8.
La variancia = n p (1 -
p ) = (14)(.2)(.8) =2.24.
 Población
finita Población
finita
Véalo
aquí
Una población finita es una población que consiste en un
número fijo de individuos, objetos o medidas conocidos.
Los ejemplos incluyen: el número de estudiantes en esta clase, el
número de automóviles en el estacionamiento.
 Distribución
hipergeométrica Distribución
hipergeométrica
Véalo
aquí
Fórmula:
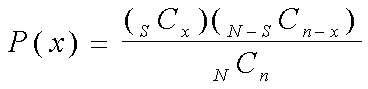
donde N es el tamaño de la población, S es el número de éxitos en
la población, x es el número de éxitos de interés, n es el tamaño
de la muestra, y C es una combinación.
Use la distribución hipergeométrica para encontrar la
probabilidad de un número específico de éxitos o fracasos si:
la muestra se selecciona de una población finita sin reemplazo
(recuerde que un criterio para la distribución binomial es que la
probabilidad de éxito es la misma de un ensayo a otro).
el tamaño de la muestra n es mayor que 5% del tamaño de la
población N.
La National Air Safety Board tiene una lista de 10 violaciones a
la seguridad reportadas por ValueJet. Suponga que sólo 4 de ellas
son en realidad violaciones y que el Safety Board sólo podrá
investigar cinco de las violaciones. ¿Cuál es la probabilidad de
que tres de las cinco violaciones seleccionadas al azar para
investigarlas sean en realidad violaciones?
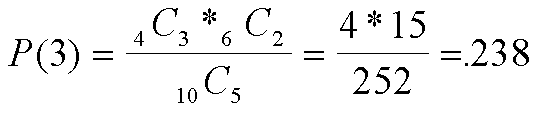 N=10
S=4
X=3
n=5
N=10
S=4
X=3
n=5
 Distribución
de Poisson Distribución
de Poisson
Véalo
aquí
La distribución de probabilidades binomial se hace cada vez más
sesgada a la derecha conforme la probabilidad de éxitos disminuye.
La forma límite de la distribución binomial donde la probabilidad
de éxito es muy pequeña y n es grande se llama distribución de
probabilidades de Poisson.
La distribución de Poisson se puede describir matemáticamente por
la fórmula:
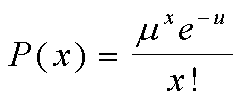
donde u es la media aritmética del número de ocurrencias en
un intervalo específico de tiempo, e es la constante
2.71828 y x es el número de ocurrencias.
El número medio de éxitos u se puede determinar en
situaciones binomiales por n p, donde n
es el número de ensayos y p la
probabilidad de éxito.
La varianza de la distribución de Poisson también es igual a n
p.
La Sylvania Urgent Care se especializa en el cuidado de
lesiones menores, resfriados y gripe. En las horas de la tarde de
6-10 PM el número medio de llegadas es 4.0 por hora.
¿Cuál es la probabilidad de 4 llegadas en una hora?
P(4) = (4^4)(e^-4)/4!=.1954.
|
|