 Definiciones
Véalo
aquí
Probabilidad: valor entre cero y uno, inclusive, que describe
la posibilidad relativa de que ocurra un evento.
Experimento: proceso que conduce a la ocurrencia de una de
varias observaciones posibles.
Resultado: lo que resulta en particular de un experimento.
Evento: conjunto de uno o más resultados de un experimento.
Enfoques de la probabilidad
Vealo
aquí
Probabilidad clásica se basa en la consideración de que los
resultados de un experimento son igualmente posibles.
Utilizando el punto de vista clásico,
Ejemplo
Considere el experimento de lanzar dos monedas al
mismo tiempo.
El espacio muestral S = {HH, HT, TH, TT}
Considere el evento de una cara.
Probabilidad de una cara = 2/4 = 1/2.
Eventos mutuamente excluyentes
Véalo
aquí
Eventos mutuamente excluyentes: la ocurrencia de cualquier
evento implica que ningún otro puede ocurrir al mismo tiempo.
En el anterior, los cuatro resultados posibles son mutuamente
excluyentes.
Eventos
colectivamente exhaustivos
Véalo
aquí
Colectivamente exhaustivos: por lo menos uno de los eventos
debe ocurrir cuando se realiza un experimento.
En el EJEMPLO, los cuatro resultados posibles son
colectivamente exhaustivos.
En otras palabras,
la suma de las probabilidades es = 1 (.25 + .25 + .25 + .25).
Concepto
de frecuencias relativas
Véalo
aquí
La probabilidad de que un evento ocurra a largo plazo se
determina observando en qué fracción de tiempo sucedieron eventos
semejantes en el pasado:
A lo largo de su carrera, la profesora Patricia ha otorgado
186 calificaciones de A entre sus 1200 estudiantes.
¿Cuál es la probabilidad de que un estudiante de su clase en
este semestre reciba una A?
Aplicando el concepto de frecuencias relativas, la
probabilidad de una A es
186 /1200 = 0.155
Probabilidad
subjetiva
Véalo
aquí
Probabilidad subjetiva: la posibilidad (probabilidad)
de que suceda un evento específico que asigna una persona con base
en cualquier información disponible.
Ejemplos de la probabilidad subjetiva son estimar la
probabilidad de que los Salgado de Salta ganen la Lotería el
próximo año y estimar la probabilidad de que ocurra un terremoto
en Los Angeles este año.
Reglas
básicas de probabilidad
Véalo
aquí
Si los eventos son mutuamente excluyentes, la ocurrencia de
cualquier evento impide que otro eventos ocurra.
Reglas de adición: si dos eventos A y B son mutuamente
excluyentes, la regla especial de adición indica que la
probabilidad de que ocurra A o B es igual a la suma de sus
probabilidades respectivas:
P(A o B) = P(A) + P(B)
Ejemplo
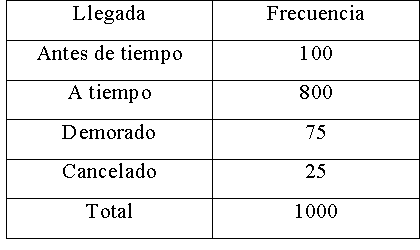
Aerolíneas Argentinas acaba de proporcionar la siguiente
información de sus vuelos de Buenos Aires a Rosario:
Ejemplo
Si A es el evento de que un vuelo llegue antes de tiempo,
entonces
P(A) = 100 /1000 = 0.1.
Si B es el evento de que un vuelo llegue demorado, entonces
P(B) = 75 /1000 = 0.075.
La probabilidad de que un vuelo llegue antes de tiempo o
demorado es
P(A o B) = P(A) + P(B) = .1 + .075 = 0.175.
Regla
del complemento
Véalo
aquí
La regla del complemento se utiliza para determinar la
probabilidad de que ocurra un evento restando del número 1 la
probabilidad de que un evento no ocurra.
Si P(A) es la probabilidad del evento A y P(~A) es el
complemento de A,
P(A) + P(~A) = 1 o P(A) = 1 - P(~A).
Diagrama de Venn que ilustra la regla del complemento
EJEMPLO
Si C es el evento de que un vuelo llegue a tiempo, entonces
P(C) = 800 /1000 = 0.8.
Si D es el evento de que un vuelo sea cancelado, entonces
P(D) = 25 /1000 = 0.025.
Utilice la regla del complemento para mostrar que la
probabilidad de que el vuelo llegue antes de tiempo (A) o demorado
(B) es 0.175.
P(A o B) = 1 - P(C o D) = 1 - [.8 + .025] = .175
Regla
general de adición
Véalo
aquí
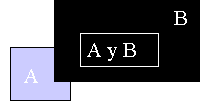
Si A y B son dos eventos que no son mutuamente excluyentes,
entonces
P(A o B) se calcula con la siguiente fórmula:
P(A o B) = P(A) + P(B) - P(A y B)
Diagrama de Venn que ilustra esta regla
Ejemplo
En una muestra de 500 estudiantes, 320 dijeron tener un
estéreo,
175 dijeron tener una TV y 100 dijeron tener ambos:
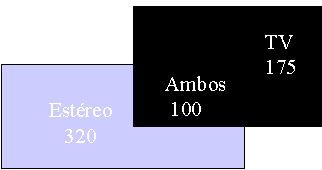Si un estudiante es seleccionado aleatoriamente,
¿cuál es la probabilidad de que tenga sólo un estéreo, sólo
una TV y uno de cada uno?
P(S) = 320 /500 = .64.
P(T) = 175 /500 = .35.
P(S y T) = 100 /500 = .20.
Si un estudiante es seleccionado aleatoriamente,
¿cuál es la probabilidad de que tenga un estéreo o una TV en
su habitación?
P(S o T) = P(S) + P(T) - P(S y T)
= .64 +.35 - .20 = .79.
Regla
especial de multiplicación
Véalo
aquí
La regla especial de multiplicación requiere que dos eventos A
y B sean independientes.
Dos eventos A y B son independientes si la ocurrencia de una no
afecta la probabililidad de ocurrencia del otro.
La regla especial se escribe: P(A y B) = P(A) * P(B).
Ejemplo
Chris posee dos inventarios independientes uno de otro.
La probabilidad de que el inventario A aumente su valor el
próximo año es .5. La probabilidad de que el B aumente el suyo es
.7.
¿Cuál es la probabilidad de que ambos aumenten su valor el
próximo año?
P(A y B) = (.5)(.7) = .35.
¿Cuál es la probabilidad de que al menos uno aumente su valor
el próximo año (esto implica que cualquiera de los dos o ambos
aumenten)?
Así, P(al menos uno) = (.5)(.3) + (.5)(.7) + (.7)(.5) = .85.
Probabilidad
conjunta
Véalo
aquí
Probabilidad conjunta es una probabilidad que mide la
posibilidad de que dos o más eventos ocurran juntos.
Un ejemplo sería el hecho de que un estudiante tenga tanto un
estéreo como una TV en su habitación.
Probabilidad
condicional
Véalo
aquí
Probabilidad condicional es la probabilidad de que ocurra un
evento en particular, dado que ocurrió otro evento.
Nota: la probabilidad de que ocurra el evento A dado que ya
ocurrió B se denota como
P(A|B).
Regla
general de multiplicación
Véalo
aquí
La regla general de multiplicación se utiliza para determina
la probabilidad conjunta de que ocurran dos eventos y establece:
para dos eventos A y B, la probabilidad conjunta que ambos
ocurran se encuentra multiplicando la probabilidad de A por la
probabilidad condicional de B dado que A ocurrió.
La probabilidad conjunta, P(A y B) está dada por la siguiente
fórmula:
P(A y B) = P(A) * P(B|A)
o
P(A y B) = P(B) * P(A|B)
Ejemplo
La directora de la escuela de administración en Miami
recolectó la siguiente información acerca de los estudiantes de
licenciatura del colegio:
Si un estudiante se selecciona al azar, ¿cuál es la
probabilidad de que el estudiante sea mujer del área de
contabilidad?
P(A y F) = 110 / 1000.
Dado que la estudiante es mujer, ¿cuál es la probabilidad que
esté en el área de contabilidad?
P(A|F) = [P(A y F)] / [P(F)] = [110 / 1000] /[400 / 1000] =
.275.
Diagrama
de árbol
Véalo
aquí
El diagrama de árbol es muy útil para visualizar las
probabilidades condicional y conjunta y en particular para el
análisis de decisiones administrativas que involucran varias
etapas.
EJEMPLO :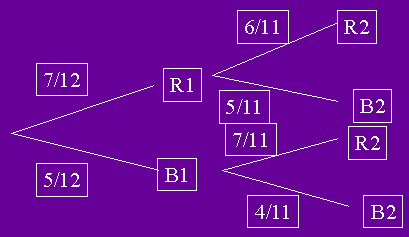
una bolsa contiene 7 fichas rojas (R) y 5 azules (B), se escogen 2
fichas, una después de la otra sin reemplazo. Construya el
diagrama de árbol con esta información.
Teorema
de Bayes
Véalo
aquí
El teorema de Bayes se representa con la fórmula:
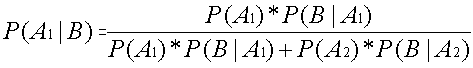
La compañía Duff Beer ha recibido varias quejas debido a que sus
botellas no van bien llenas.
Una queja fue recibida hoy pero el gerente de producción no
puede identificar cuál de las dos plantas Springfield (A o B)
llenó esta botella.
¿Cuál es la probabilidad de que la botella mal llenada haya
salido de la planta A?
P(A |U) = [(.55)(.03)]/[(.55)(.03) + (.45)(.04)] = .4783.
Algunos
principios de conteo
Véalo
aquí
Fórmula de la multiplicación: si hay m modos de hacer una cosa
y n formas de hacer otra, existen m x n formas de hacer ambas.
EJEMPLO: el Doctor Périssé tiene 10 camisas y 8 corbatas.
¿Cuántos conjuntos de camisas /corbatas tiene?
(10)(8) = 80.
Permutación: un arreglo de r objetos seleccionados a partir de
un grupo único de n objetos posibles.
Nota: el orden del arreglo es importante en las permutaciones.
Combinación: el número de modos para elegir r objetos de un
grupo de n objetos sin considerar el orden.
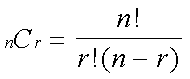Ejemplo
El entrenador Alexis tiene que elegir 5 jugadores entre los
doce del equipo para incluirlos en alineación.
¿Cuántos grupos diferentes se pueden formar?
12C5 = (12!)/[5!(12-5)!] =792
Suponga que el entrenador Alexis debe clasificarlos en orden:
12P5 = (12!)/(12-5)! = 95,040.
|
