|
|
|
 Desviación
media Desviación
media
Véalo
aquí
Desviación media: media aritmética de los valores absolutos de
las desviaciones respecto a la media aritmética.
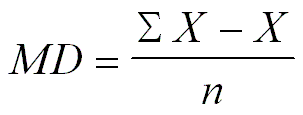 Ejemplo:
Los pesos de una muestra de cajas con frenos en un taller son
(en Kg.)
103, 97, 101, 106 y 103.
Ejemplo:
Los pesos de una muestra de cajas con frenos en un taller son
(en Kg.)
103, 97, 101, 106 y 103.
`C = 510/5 = 102 Kg.
S = 1 + 5 + 1 + 4 + 1 = 12
MD = 12/5 = 2.4
Por lo común los pesos de las cajas están a 2.4 Kg del peso medio
de 102 Kg.
 Variancia de la población
Variancia de la población
Vealo
aquí
La varianza de la población para datos no agrupados es la
media aritmética de las desviaciones cuadráticas respecto a la
media de la población.
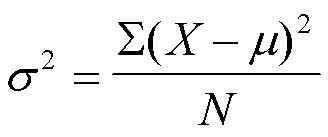 Ejemplo:
Las edades de la familia Orduz son 2, 18, 34, y 42 años. ¿Cuál
es la variancia de la población?
Ejemplo:
Las edades de la familia Orduz son 2, 18, 34, y 42 años. ¿Cuál
es la variancia de la población?
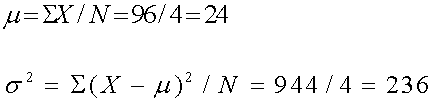 Una fórmula alternativa para la variancia poblacional es:
Una fórmula alternativa para la variancia poblacional es:
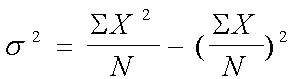
 Desviación estándar poblacional
Desviación estándar poblacional
Véalo
aquí
La desviación estándar poblacional (σ) es la raíz cuadrada de
la variancia de la población.
Para el ejemplo anterior, la desviación estándar poblacional
es 15.19 (raíz cuadrada de 230.81).
 Variancia
muestral Variancia
muestral
Véalo
aquí
La variancia muestral estima la variancia de la población.
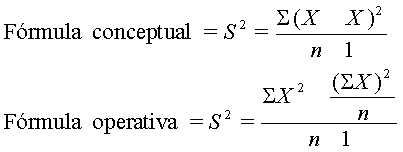 Ejemplo:
Una muestra de cinco salarios por hora para varios trabajos en
el área es: $7, $5, $11, $8, $6.
Encuentre la variancia.
X = 37/5 = 7.40
Ejemplo:
Una muestra de cinco salarios por hora para varios trabajos en
el área es: $7, $5, $11, $8, $6.
Encuentre la variancia.
X = 37/5 = 7.40
S2= 21.2/(5-1) = 5.3
 Desviación
estándar muestral Desviación
estándar muestral
Véalo
aquí
La desviación estándar muestral es la raíz cuadrada de la
variancia muestral.
En el ejercicio anterior, la desviación estándar de la muestra
es = 2.30
 Medidas
de dispersión: datos no agrupados Medidas
de dispersión: datos no agrupados
Véalo
aquí
Para datos no agrupados, la amplitud es la diferencia entre
los valores mayor y menor en un conjunto de datos.
AMPLITUD = valor mayor - valor menor
Ejemplo: una muestra de cinco graduados de contaduría indicó
los siguientes salarios iniciales:
$22 000, $28 000, $31 000, $23 000, $24 000.
La amplitud es $31 000 - $22 000 = $9 000.
 Variancia
muestral para datos agrupados Variancia
muestral para datos agrupados
Véalo
aquí
La fórmula de la variancia para datos agrupados usada como
estimador de la variancia poblacional es:
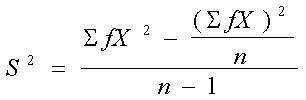
donde f es la frecuencia de clase y X es el punto medio de la
clase.
 Interpretación
y usos de la desviación estándar Interpretación
y usos de la desviación estándar
Véalo
aquí
Teorema de Chebyshev: para cualquier conjunto de
observaciones, la proporción mínima de valores que está dentro de
k desviaciones estándar desde la media es al menos 1 - 1/k , donde
k2 es una constante mayor que 1.
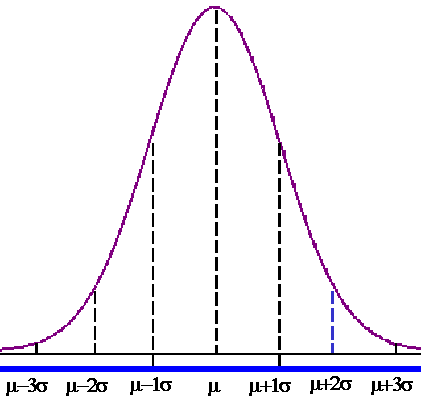
Regla empírica: para una distribución de frecuencias
simétrica de campana, cerca de 68% de las observaciones estará
dentro de ±1σ de la media (μ); cerca de 95% de las observaciones
estará dentro de ±2σ de la media (μ); alrededor de 99.7% estará
dentro de ±3σ de la media (μ).
 Dispersión
relativa Dispersión
relativa
Véalo
aquí
El coeficiente de variación es la razón de la desviación
estándar a la media aritmética, expresada como porcentaje:
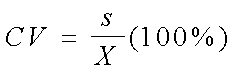
 Asimetría Asimetría
Véalo
aquí
Asimetría (sesgo) es la medida de la falta de simetría en una
distribución.
El coeficiente de asimetría se calcula mediante la siguiente
fórmula:
Sk = 3(media - mediana) /desviación estándar
 Amplitud
intercuartílica Amplitud
intercuartílica
Véalo
aquí
La amplitud intercuartílica es la distancia entre el tercer
cuartil Q3 y el primer cuartil Q1.
Amplitud intercuartílica = tercer cuartil - primer cuartil =
Q3 - Q1
 Primer
cuartil Primer
cuartil
Véalo
aquí
El primer cuartil es el valor correspondiente al punto debajo
del cual se encuentra el 25% de las observaciones en un conjunto
ordenado de datos.
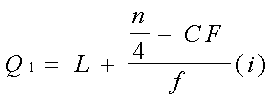
donde L = límite de las clases que contienen Q1, CF = frecuencia
acumulada que precede a la clase que contiene a Q1, f = frecuencia
de la clase que contiene Q1, i= tamaño de la clase que contiene
Q1.
 Tercer
cuartil Tercer
cuartil
Véalo
aquí
El tercer cuartil es el valor correspondiente al punto debajo
del cual se encuentra 75% de las observaciones en un conjunto
ordenado de datos:
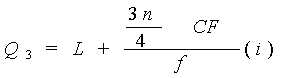
donde L = límite inferior de la clase que contiene a Q3, CF =
frecuencia acumulada precedente a la clase que contiene a Q3, f =
frecuencia de la clase que contiene a Q3, i = tamaño de la clase
que contiene a Q3
 Desviación
cuartílica Desviación
cuartílica
Véalo
aquí
La desviación cuartílica es la mitad de la distancia entre el
tercer cuartil, Q3, y el primero, Q1.
QD = [Q3 - Q1]/2
Ejemplo:
Si el tercer cuartil = 24 y el primer cuartil = 10,
¿cuál es la desviación cuartílica?
La amplitud intercuartílica es 24 - 10 = 14;
por lo tanto,
la desviación cuartílica es 14/2 = 7.
 Amplitud
cuartílica Amplitud
cuartílica
Véalo
aquí
Cada conjunto de datos tiene 99 percentiles, que dividen el
conjunto en 100 partes iguales.
La amplitud cuartílica es la distancia entre dos percentiles
establecidos.
La amplitud cuartílica 10 a 90 es la distancia entre el 10º y
90º percentiles.
 Fórmula
para porcentiles Fórmula
para porcentiles
Véalo
aquí
 Diagramas
de caja Diagramas
de caja
Véalo
aquí
Un diagrama de caja es una ilustración gráfica, basada en
cuartiles, que ayuda a visualizar un conjunto de datos.
Se requieren cinco tipos de datos para construir un diagrama
de caja: el valor mínimo, el primer cuartil, la mediana, el tercer
cuartil, y el valor máximo.
Ejemplo:
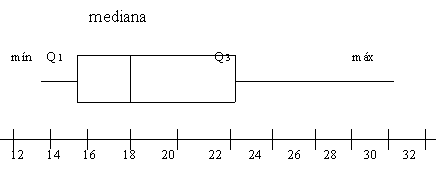
Con base en una muestra de 20 entregas, Marco’s Pizza
determinó la siguiente información:
valor mínimo = 13 minutos,
Q1 = 15 minutos,
mediana = 18 minutos,
Q3 = 22 minutos,
valor máximo = 30 minutos.
Desarrolle un diagrama de caja para los tiempos de entrega.
|
|