|
|
|
 Desviación
media Desviación
media
Véalo
aquí
Para datos no agrupados, la media de la población es la suma
de todos los valores en ella dividida entre el total de valores en
la población:
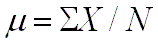
donde µ representa la media de la población.
N es el número total de elementos en la población.
X representa cualquier valor en particular.
∑ indica la operación de sumar.
Ejemplo
Parámetro: una característica de una población.
La familia Orduz posee cuatro autos. Los datos son los
kilómetros recorridos por cada uno: 56 000, 23 000, 42 000 y
73 000. Encuentre el promedio de kilómetros de los cuatro autos.
Esto es (56 000 + 23 000 + 42 000 + 73 000)/4 = 48 500
 Media de una muestra
Media de una muestra
Vealo
aquí
Para datos no agrupados, la media de una muestra es la suma de
todos los valores divididos entre el número total de los mismos:

donde
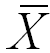 denota
la media muestral denota
la media muestral
N es el número total de valores en la muestra.
Ejemplo:
Dato estadístico: una característica de una
muestra.
Una muestra de cinco ejecutivos recibió la siguiente cantidad en
bonos el año pasado: $14000, $15000, $17000, $16000 y $15000.
Encuentre el promedio en bonos para los cinco
ejecutivos.
Como estos valores representan la muestra de 5
ejecutivos, la media de la muestra es
(14000 + 15000 + 17000 + 16000 + 15000) / 5 = $15400.
 Propiedades de la media aritmética
Propiedades de la media aritmética
Véalo
aquí
- Todo conjunto de datos de nivel de intervalo y de nivel de
razón tiene un valor medio.
- Al evaluar la media se incluyen todos los valores.
- Un conjunto de valores sólo tiene una media.
- La cantidad de datos a evaluar rara vez afecta la media.
- La media es la única medida de ubicación donde la suma de
las desviaciones de cada valor con respecto a la media, siempre
es cero.
Ejemplo:
-
Considere el conjunto de valores: 3, 8 y 4. La
media es 5.
-
Para ilustrar la quinta propiedad,
-
(3 - 5) + (8 - 5) + (4 - 5) = - 2 + 3 - 1 = 0.
-
En otras palabras,
-
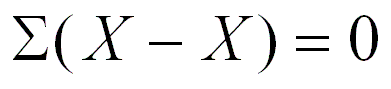
 Media ponderada
Media ponderada
Véalo
aquí
La media ponderada de un conjunto de números X1, X2, ..., Xn,
con las ponderaciones correspondientes w1, w2, ...,wn, se calcula
con la fórmula:
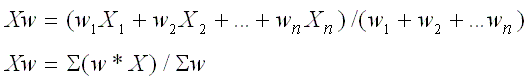 Ejemplo:
Durante un periodo de una hora en una tarde calurosa de un
sábado, el cantinero Julio sirvió cincuenta bebidas.
Calcule la media ponderada de los precios de las bebidas.
(Precio ($), cantidad vendida): (.50,5), (.75,15), (.90,15),
(1.10,15).
La media ponderada es:
$(.50 x 5 + .75 x 15 + .90 x 15 + 1.10 x 15) / (5 + 15 + 15 +
15) =
$43.75/50 = $0.875
Ejemplo:
Durante un periodo de una hora en una tarde calurosa de un
sábado, el cantinero Julio sirvió cincuenta bebidas.
Calcule la media ponderada de los precios de las bebidas.
(Precio ($), cantidad vendida): (.50,5), (.75,15), (.90,15),
(1.10,15).
La media ponderada es:
$(.50 x 5 + .75 x 15 + .90 x 15 + 1.10 x 15) / (5 + 15 + 15 +
15) =
$43.75/50 = $0.875
 Mediana Mediana
Véalo
aquí
Mediana: es el punto medio de los valores después de
ordenarlos de menor a mayor, o de mayor a menor. La misma cantidad
de valores se encuentra por arriba de la mediana que por debajo de
ella.
Nota: para un conjunto con un número par de números, la
mediana será el promedio aritmético de los dos números medios.
Ejemplo:
Calcule la mediana para los siguientes datos.
La edad de una muestra de cinco estudiantes es: 21, 25, 19, 20
y 22.
Al ordenar los datos de manera ascendente quedan: 19, 20, 21, 22,
25.
La mediana es 21.
 Propiedades
de la mediana Propiedades
de la mediana
Véalo
aquí
- La mediana es única para cada conjunto de datos.
- No se ve afectada por valores muy grandes o muy pequeños, y
por lo tanto es una medida valiosa de tendencia central cuando
ocurren.
- Puede obtenerse para datos de nivel de razón, de intervalo y
ordinal.
- Puede calcularse para una distribución de frecuencias con
una clase de extremo abierto, si la mediana no se encuentra en
una de estas clases.
 Moda Moda
Véalo
aquí
La moda es el valor de la observación que aparece con más
frecuencia.
Ejemplo:
las calificaciones de un examen de diez estudiantes son:
81, 93, 84, 75, 68, 87, 81, 75, 81, 87.
Como la calificación 81 es la que más ocurre, la calificación
modal es 81.
 Media
geométrica Media
geométrica
Véalo
aquí
La media geométrica (MG) de un conjunto de n números positivos
se define como la raíz n-ésima del producto de los n valores. Su
fórmula es:
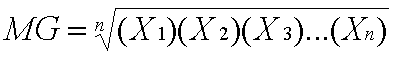 La media geométrica se usa para encontrar el promedio de
porcentajes, razones, índices o tasas de crecimiento.
Ejemplo
Las tasas de interés de tres bonos son 5%, 7% y 4%.
La media geométrica es
La media geométrica se usa para encontrar el promedio de
porcentajes, razones, índices o tasas de crecimiento.
Ejemplo
Las tasas de interés de tres bonos son 5%, 7% y 4%.
La media geométrica es
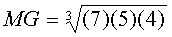 =
5.192.
La media aritmética es (6 + 3 + 2)/3 = 5.333.
La MG da una cifra de ganancia más conservadora porque no
tiene una ponderación alta para la tasa de 7%.
Otra aplicación de la media geométrica es determinar el
porcentaje promedio del incremento en ventas, producción u otros
negocios o series económicas de un periodo a otro.
La fórmula para este tipo de problema es: =
5.192.
La media aritmética es (6 + 3 + 2)/3 = 5.333.
La MG da una cifra de ganancia más conservadora porque no
tiene una ponderación alta para la tasa de 7%.
Otra aplicación de la media geométrica es determinar el
porcentaje promedio del incremento en ventas, producción u otros
negocios o series económicas de un periodo a otro.
La fórmula para este tipo de problema es:
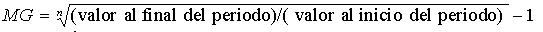 Ejemplo
El número total de mujeres inscritas en colegios americanos
aumentó de 755 000 en 1986 a 835 000 en 1995.
Aquí n = 10, así (n - 1) = 9.
Ejemplo
El número total de mujeres inscritas en colegios americanos
aumentó de 755 000 en 1986 a 835 000 en 1995.
Aquí n = 10, así (n - 1) = 9.
Es decir, la media geométrica de la tasa de crecimiento es 1.27%.
 Media
de datos agrupados Media
de datos agrupados
Véalo
aquí
La media de una muestra de datos organizados en una
distribución de frecuencias se calcula mediante la siguiente
fórmula:
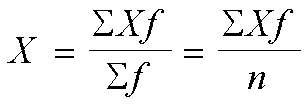 Ejemplo:
Una muestra de diez cines en una gran área metropolitana dio
el número total de películas exhibidas la semana anterior.
Calcule la media de las películas proyectadas.
Ejemplo:
Una muestra de diez cines en una gran área metropolitana dio
el número total de películas exhibidas la semana anterior.
Calcule la media de las películas proyectadas.
Películas
exhibidas |
Frecuencia,
f |
Punto medio
de clase X |
(f)(X) |
| 1-2 |
1 |
1.5 |
1.5 |
| 3-4 |
2 |
3.5 |
7.5 |
| 5-6 |
3 |
5.5 |
16.5 |
| 7-8 |
1 |
7.5 |
7.5 |
| 9-10 |
3 |
9.5 |
28.5 |
| total |
10 |
|
61 |
61/10 = 6.1 películas
 Mediana de datos agrupados
Mediana de datos agrupados
Véalo
aquí
La mediana de una muestra de datos organizados en una
distribución de frecuencias se calcula mediante la siguiente
fórmula:Mediana = L + [(n/2 - FA)/f] (i)
donde L es el límite inferior de la clase que contiene a la
mediana, FA es la frecuencia acumulada que precede a la clase de
la mediana, f es la frecuencia de clase de la mediana e i es el
intervalo de clase de la mediana.
Para determinar la clase de la mediana de datos agrupados:
Elabore una distribución de frecuencias acumulada.
Divida el número total de datos entre 2.
Determine qué clase contiene este valor.
Por ejemplo, si n=50, 50/2 = 25, después determine qué clase
contiene el 25° valor (la clase de la mediana).
| Películas
exhibidas |
Frecuencia |
Frecuencia
acumulada |
| 1-2 |
1 |
1 |
| 3-4 |
2 |
3 |
| 5-6 |
3 |
6 |
| 7-8 |
1 |
7 |
| 9-10 |
3 |
10 |
La clase de la mediana es 5 - 6, ya que contiene el 5° valor
(n/2 = 5)
De la tabla, L = 5, n = 10, f = 3, i = 2, FA = 3.
Así, mediana = 5 + [((10/2) - 4)/3](2) = 6.33
 Moda
de datos agrupados Moda
de datos agrupados
Véalo
aquí
La moda de los datos agrupados se aproxima por el punto medio
de la clase que contiene la frecuencia de clase mayor.
Las modas en el ejemplo de la Mediana de datos agrupados son
5.5 y 9.5. Cuando dos valores ocurren una gran cantidad de veces,
la distribución se llama bimodal, como en dicho ejemplo.
 Distribución:
simétrica, con asimetría positiva, con asimetría negativa Distribución:
simétrica, con asimetría positiva, con asimetría negativa
Véalo
aquí
Distribución simétrica :
sesgo cero moda = mediana = media
 Distribución con asimetría positiva:
sesgo a la derecha: media y mediana se encuentran a la derecha
de la moda.
Distribución con asimetría positiva:
sesgo a la derecha: media y mediana se encuentran a la derecha
de la moda.
moda < mediana < media
 Distribución con asimetría negativa:
sesgo a la izquierda: media y mediana están a la
izquierda de la moda.
media < mediana < moda
Distribución con asimetría negativa:
sesgo a la izquierda: media y mediana están a la
izquierda de la moda.
media < mediana < moda

Nota
Si se conocen dos promedios de una distribución
de frecuencias con sesgo moderado, el tercero se puede aproximar.
moda = media - 3(media - mediana)
media = [3(mediana) - moda]/2
mediana = [2(media) + moda]/3
|
|