Breviario de Ciencia e Investigación Científica
Teoría y Leyes
Hablaremos sobre las teorías, lo haremos en dos partes; en la primera veremos qué son las teorías y cuáles son sus elementos constitutivos, en la segunda parte hablaremos de cómo podemos hacer una teoría o una ley, ya que como científicos buscamos saber qué cosas están mal, o qué es lo que falta, y así crear nuestro espacio de investigación.
Teorías
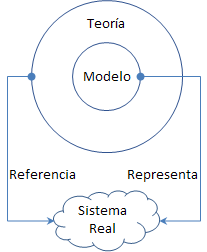
Teorías: que son
Coloquialmente algunas personas opinan que las teorías son una descripción de la realidad, las cuales pueden ser descripciones de percepciones o de los datos de los sentidos; en tanto para otras, una teoría, es una "verdadera" explicación de los hechos.
En el libro titulado La evolución de la física, Albert Einstein dijo:
El objeto de toda teoría física, es la explicación del más amplio conjunto de fenómenos posible; y agregó: se justifica, mientras nos hace inteligibles los sucesos de la naturaleza.
Teorías: elementos constitutivos
Una teoría abarca los siguientes elementos constitutivos
- conceptos primitivos,
- axiomas,
- postulados, y
- demostraciones.
«Conceptos primitivos» (básicos o fundamentales): so pena del problema de la regresión infinita, las teorías no pueden dejar de prescindir de los conceptos primitivos; sus términos son consensuados, y todos admitimos que tenemos la misma concepción sobre ellos, como en el caso: del espacio, el punto, la recta, y el plano. Para ejemplificarlo, imaginemos el siguiente diálogo entre dos personas:
- Me podrías decir qué es un «triángulo»,
- un «triángulo» es un «polígono» de tres segmentos que determinan tres puntos del plano no colineales.
- Qué es un «polígono»,
- un «polígono» es una figura geométrica plana, compuesta por una secuencia finita de «segmentos» rectos consecutivos, que encierran una región en el plano.
- Qué es un «segmento»,
- un «segmento» es un fragmento de recta que está comprendido entre dos «puntos», llamados «puntos extremos o finales».
- Qué es un «punto»,
- un «punto» es una unidad indivisible. El «punto» es una figura geométrica sin dimensión; por tanto, no tiene longitud, área, volumen, ni otro ángulo dimensional, entonces no es un objeto físico; con respecto de un sistema de coordenadas preestablecidas, describe una posición determinada en el espacio.
En este ejemplo, vemos que, sin la aceptación de los enunciados básicos, cualquier definición nos podría llevar a una regresión infinita.
«Axiomas»: son principios generales que no precisan ser probados para la ciencia. Tomemos dos ejemplos:
- el primero de Los Elementos de Euclides: dos puntos cualesquiera determinan un segmento de recta;
- el segundo de los Axiomas de Peano y de la teoría de conjuntos de Bertrand Ruessell: Todo número natural tiene su subsiguiente.
«Postulados» o definiciones implícitas: podremos considerarlos como los teoremas iniciales de una cadena deductiva. Tomemos un ejemplo del libro Los elementos de Euclides, en el cual se muestra cómo, a partir de tres postulados, se obtiene la derivación de una definición:
- Postulado: Un punto es lo que no tiene partes (Libro I, definición 1). •
- Postulado: Una línea es una longitud sin anchura (Libro I, definición 2). —
- Postulado: Los extremos de una línea son puntos (Libro I, definición 3). ⋅—⋅
∴ Definición: Una línea recta es aquella que yace por igual respecto de los puntos que están en ella (Libro I, definición 4). ⁄
Aquí hagamos una pausa y comparemos a este ejemplo, con el ejemplo de los axiomas, para el cuál habíamos simulado un diálogo que al fin expuso a una noción racional como un cúmulo de conocimientos, en tanto aquí se expone al conocimiento como un encadenamiento de ideas; lo que nos pone ante dos concepciones epistemológicas de la ciencia: como cúmulo o como encadenamiento de ideas.
«Demostraciones»: veámoslas con este ejemplo basado en el siguiente postulado:
La suma de los ángulos interiores de un triángulo es igual a dos rectos. Δ
Euclides lo demuestra de la siguiente manera con su Proposición 32 en el libro I de los Elementos:
en un triángulo, si se prolonga uno de los lados, el ángulo externo es igual a los dos ángulos internos y opuestos, y los tres ángulos internos del triángulo son iguales a dos rectos (Elementos, Libro I, 32) Δ__
Este ejemplo lo utilizaba Spinoza, en su Tratado breve, para mostrar cómo una idea lleva a otra y su unión implica la existencia de ambas.
Cómo elaborar una Ley
Hasta aquí ya vimos qué es una teoría, ahora veamos la manera de buscar una Ley; para ello nos basaremos en las explicaciones sobre el método científico de Richard Feynman, que lo cuenta de la siguiente manera:
- primero, tenemos que hacer una suposición mediante un conjunto de enunciados, para que se presente como una explicación verosímil; después, para ver qué implicaría
- calculamos las consecuencias de nuestro supuesto; y luego, para ver si funcionan
- comparamos nuestros cálculos con los hechos fácticos; o sea, por medio de la experimentación, observamos nuevamente a la naturaleza; solo que ahora, con el saber construido.
Ahora bien, si nuestros cálculos presentan una discrepancia con los resultados del experimento, entonces… el supuesto… está mal; y ésta es la clave de la ciencia, no tiene importancia el glamur de un supuesto, lo inteligente o importante que sea la persona que lo propone, si está en desacuerdo con el experimento, la suposición está mal.
Ahora, pensemos en que hacemos una buena suposición, calculamos las consecuencias, y descubrimos que todas ellas coinciden con nuestros experimentos; pregunta: ¿la teoría, es correcta?... no; simplemente no hemos probado que es incorrecta, ya que, en el futuro, podría haber un rango más amplio de experimentos, que implique computar un rango más amplio de consecuencias, y ahí pueden descubrir que la teoría es incorrecta.
Si lo piensan, verán que inicialmente, con esta metodología, alcanzaremos una teoría definida; pero además, a cualquier teoría ya definida, siempre la podremos probar como incorrecta; así es que solamente vamos a estar seguros, cuando estemos ante una teoría incorrecta; pero esto no quita que se puedan elaborar teorías y leyes como ideas racionales que duren un largo tiempo.
También debemos apuntar a que no podremos probar que una teoría es incorrecta, si el supuesto en la que se basa es vago o está pobremente expresado, explicando más o menos como funciona; porque además, si el proceso de computar las consecuencias es indefinido o indeterminado, entonces con algo de habilidad, cualquier resultado experimental puede hacerse ver como una consecuencia esperada. Entonces, pueden ver que una teoría podría ser presentada engañosamente buena, porque por su vaguedad no se puede probar incorrecta. Así que: teniendo una teoría vaga, es posible obtener cualquier resultado.
Bien, en referencia al problema de investigación, hasta aquí vimos la importancia de que el supuesto esté lo más definido posible y que sea consistente con los experimentos, independientemente de cuál sea su origen.
Visto todo esto, verán que la primera dificultad es cómo empezar, y para ello podemos analizar si "todos los principios conocidos" son consistentes; si fueran inconsistentes unos con otros, algo debe ser cambiado; así es que, profundizaremos las evidencias existentes para encontrar huecos o hacerlos a fin de crear un espacio para nuevos supuestos…
Como corolario diremos que:
Para toda comunidad científica, apuntalar los conceptos claros y obvios, no sirve de nada; tampoco sirve problematizar lo que es incorrecto, pues lo que precisamente debemos saber es lo que va a ser sustituido en su lugar. Entonces, el problema no es decir que algo esté mal o un supuesto esté equivocado, lo difícil será el remplazarlo por un supuesto consistente.